练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，点O在直线PQ上，∠AOP=20°，将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′，且有∠B′O′Q=40°，则∠AOB的度数为（　　）
    A．120°B．140°C．150°D．160°

    分析 根据平移的性质得到AO∥A′O′，OB∥O′B′，由平行线的性质得到同位角相等，根据平角的定义即可得到结果．

    解答 解：∵将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′，
    ∴AO∥A′O′，OB∥O′B′，
    ∴∠BOO′=∠B′O′Q=40°，
    ∴∠AOB=180°-∠AOP-∠BOP′=180°-20°-40°=120°，
    故选A．

    点评 本题考查了平移的性质，平行线的性质，平角的定义，熟练掌握平移的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．在向红星镇居民介绍王家庄位置的时候，我们可以这样说：如图1，在以红星镇为原点，正东方向为x轴正方向，正北方向为y轴正方向的平面直角坐标系（1单位长度表示的实际距离为1km）中，王家庄的坐标为（5，5）；也可以说，王家庄在红星镇东北方向$\sqrt{50}$km的地方．

    还有一种方法广泛应用于航海、航空、气象、军事等领域．如图2：在红星镇所建的雷达站O的雷达显示屏上，把周角每15°分成一份，正东方向为0°，相邻两圆之间的距离为1个单位长度（1单位长度表示的实际距离为1km），现发现2个目标，我们约定用（10，15°）表示点M在雷达显示器上的坐标，则：
    （1）点N可表示为（8，135°）；王家庄位置可表示为（$\sqrt{50}$，45°）；点N关于雷达站点0成中心对称的点P的坐标为（8，315°）；
    （2）S△OMP=20$\sqrt{3}$km2；
    （3）若有一家大型超市A在图中（4，30°）的地方，请直接标出点A，并将超市A与雷达站O连接，现准备在雷达站周围建立便民服务店B，使得△ABO为底角30°的等腰三角形，请直接写出B点在雷达显示屏上的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

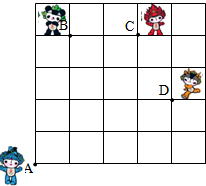    3．如图，奥运福娃在5×5的方格（每小格边长为1m）上沿着网格线运动．贝贝从A处出发去寻找B、C、D处的其它福娃，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（-1，-4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中
    （1）A→D（+4，+2），B→C（+2，0），C→A（-3，-4）；
    （2）若贝贝的行走路线为A→B→C→D，请计算贝贝走过的路程；
    （3）若贝贝从A处去寻找妮妮的行走路线依次为（+1，+2），（+2，-1），（-2，+3），（1，-2），请在图中标出妮妮的位置E点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．在平面直角坐标系中，点P（m，-m）（m≠0）在第二、四象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．函数y=k${x}^{{k}^{2}-3}$是反比例函数，则k的值是（　　）
    A．-1B．2C．±2D．±$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

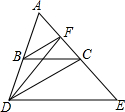    17．如图，已知BC∥DE，BF平分∠ABC，DC平分∠ADE，则下列判断：①∠ACB=∠E；②DF平分∠ADC；③∠BFD=∠BDF；④∠ABF=∠BCD中，正确的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图是一组密码的一部分，为了保密，许多情况下可采用不同的密码，请你运用所学数学知识找到破译密码的“钥匙”，目前，已破译处“正做数学”的真实意义是“”祝你成功，若“正”所处的位置为（x，y），你找到的密码钥匙是（x-1，y-2），破译的“今天考试”真实意思是努力发挥．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知方程x2+px+q=0有两个相同的实数根，判断方程x2-p（1+q）x+q3+2q2+q=0的根情况．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知正方形ABCD，顶点A与坐标原点重合，顶点B、D分别在x轴和y轴的正半轴上，顶点C在反比例函数y=$\frac{16}{x}$（x＞0）的图象上，如图所示，动点P以每秒1个单位的速度从A点出发沿AB方向运动，动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动，当点P与点Q相遇时停止运动，设点P的运动时间为t．
    （1）求该正方形的边长；
    （2）当点Q在边CB上运动时，用含t的代数式表示以点Q、P、D为顶点的三角形的面积S，并求出自变量t的取值范围；
    （3）连接PD，当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时，求点Q的坐标．

    查看答案和解析>>

    同步练习册答案