
 已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=$\frac{1}{2}$,则AB=$\sqrt{5}$,sin∠ABE=$\frac{4}{5}$.
已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=$\frac{1}{2}$,则AB=$\sqrt{5}$,sin∠ABE=$\frac{4}{5}$. 分析 (1)首先连接AC,AC与BD相交于点O,由四边形ABCD是菱形,可得AC⊥BD,BO=$\frac{1}{2}$BD=2,又由tan∠CBD=$\frac{1}{2}$,可求得OC的长,然后由勾股定理求得边AB的长;
(2)由AE⊥BC,利用S菱形ABCD=BC•AE=$\frac{1}{2}$BD•AC,即可求得AE的长,继而求得∠ABE的正弦值.
解答  解:(1)连接AC,AC与BD相交于点O,
解:(1)连接AC,AC与BD相交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,BO=$\frac{1}{2}$BD=2,
∵Rt△BOC中,tan∠CBD=$\frac{OC}{OB}$=,
∴OC=1,
∴AB=BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$;
(2)∵AE⊥BC,
∴S菱形ABCD=BC•AE=$\frac{1}{2}$BD•AC,
∵AC=2OC=2,
∴$\sqrt{5}$AE=$\frac{1}{2}$×2×4,
∴AE=$\frac{4\sqrt{5}}{5}$,
∴sin∠ABE=$\frac{AE}{AB}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 此题考查了菱形的性质、勾股定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:选择题

| A. | 62 | B. | 70 | C. | 84 | D. | 108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
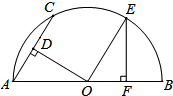 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{6}$ | B. | x6÷x3=x2 | C. | $\sqrt{4}$=2 | D. | a2(-a2)=a4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.25×107 | B. | 8.25×106 | C. | 82.5×105 | D. | 0.825×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,某工人师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面,且要使大正方形的边长比小正方形的边长大1m.求裁剪后剩下的阴影部分的面积.
如图所示,某工人师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面,且要使大正方形的边长比小正方形的边长大1m.求裁剪后剩下的阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com