
【题目】如图抛物线![]() 的开口向下与
的开口向下与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点(不与点
是抛物线上一个动点(不与点![]() 重合)
重合)

(1)求抛物线的解析式;
(2)当点![]() 是抛物线上一个动点,若
是抛物线上一个动点,若![]() 的面积为12,求点
的面积为12,求点![]() 的坐标;
的坐标;
(3)如图2,抛物线的顶点为![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() ,若存在请直接写出点
,若存在请直接写出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
【答案】(1)![]() ;(2)点P的坐标为(2,8)或(4,6)或(3
;(2)点P的坐标为(2,8)或(4,6)或(3![]() ,
,![]() 1)或(3+
1)或(3+![]() ,
,![]() 1);(3)点E坐标为(
1);(3)点E坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)将点![]() 和点
和点![]() 代入
代入![]() 求出a,b即可;
求出a,b即可;
(2)如图作辅助线,根据S△PCA=![]() PG×AC=
PG×AC=![]() ×
×![]() HP×
HP×![]() =12求出HP=4,由直线AC的表达式为y=x+6可得直线m的表达式,然后求出直线m和抛物线的交点即可得到两个P点坐标,同理可得直线n的表达式,进而得出另外两个P点坐标;
=12求出HP=4,由直线AC的表达式为y=x+6可得直线m的表达式,然后求出直线m和抛物线的交点即可得到两个P点坐标,同理可得直线n的表达式,进而得出另外两个P点坐标;
(3)首先证明∠ACD=90°,可得sin∠DAC=![]() ,然后作辅助线构造三角形,求出sin2∠DAC=
,然后作辅助线构造三角形,求出sin2∠DAC=![]() ,进而可得tan∠EAB=
,进而可得tan∠EAB=![]() ,然后分情况讨论:①当点E在AB上方时,求出直线AE的表达式即可解决问题,②当点E在AB下方时,同理计算即可.
,然后分情况讨论:①当点E在AB上方时,求出直线AE的表达式即可解决问题,②当点E在AB下方时,同理计算即可.
解:(1)将点![]() 和点
和点![]() 代入
代入![]() 得:/span>
得:/span>![]() ,
,
解得: ,
,
∴抛物线的解析式为:![]() ;
;
(2)如图1所示,过点P作直线m∥AC交抛物线于点P′,在直线AC下方等距离处作直线n交抛物线于点P″、P′″,过点P作PH∥y轴交AC于点H,作PG⊥AC于点G,

∵抛物线的解析式为:![]() ,
,
∴C(0,6),
∴OA=OC,
∴∠PHG=∠ACB=45°,则HP=![]() PG,
PG,
∴S△PCA=![]() PG×AC=
PG×AC=![]() ×
×![]() HP×
HP×![]() =12,
=12,
解得:HP=4,
易得直线AC的表达式为:y=x+6,
则直线m的表达式为:y=x+10,
联立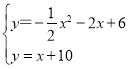 ,解得:
,解得:![]() 或
或![]() ,
,
∴点P坐标为(2,8)或(4,6);
同理可得,直线n的表达式为:y=x+2,点P(P″、P′″)的坐标为(3![]() ,
,![]() 1)或(3+
1)或(3+![]() ,
,![]() 1),
1),
综上,点P的坐标为(2,8)或(4,6)或(3![]() ,
,![]() 1)或(3+
1)或(3+![]() ,
,![]() 1);
1);
(3)∵![]() ,
,
∴D(2,8),
∵点A(6,0)、B(2,0)、C(0,6),
∴AC2=![]() ,CD2=
,CD2=![]() ,AD2=
,AD2=![]() ,
,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴sin∠DAC=![]() ,
,
如图2,延长DC至D′使CD=CD′,连接AD′,过点D作DH⊥AD′,

则DD′=2CD=![]() ,AD=AD′=
,AD=AD′=![]() ,
,
∵S△ADD′=![]() ×DD′×AC=
×DD′×AC=![]() DH×AD′,
DH×AD′,
∴![]() ×
×![]() ×
×![]() =
=![]() DH×
DH×![]() ,
,
解得:DH=![]() ,
,
∴sin2∠DAC=sin∠DAD′=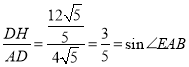 ,
,
易得tan∠EAB=![]() ,
,
①当点E在AB上方时,如图3,
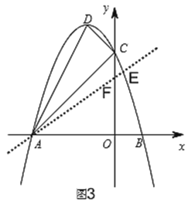
设直线AE交y轴于F,
则tan∠EAB=![]() ,
,
∴OF=![]() ,即F(0,
,即F(0,![]() ),
),
设直线AE的表达式为:y=kx+![]() ,
,
代入A(-6,0)解得:![]() ,
,
∴直线AE的表达式为:y=![]() x+
x+![]() ,
,
联立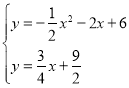 ,解得:
,解得:![]() 或
或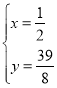 ,
,
∴点E坐标为(![]() ,
,![]() );
);
②当点E在AB下方时,
同理可得:点E(![]() ,
,![]() ),
),
综上,点E坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】小明对九(1)、九(2)班(人数都为50人)参加“阳光体育”的情况进行了调查,统计结果如图所示.下列说法中正确的是( )
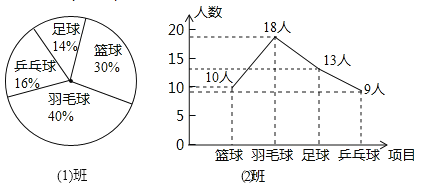
A.喜欢乒乓球的人数(1)班比(2)班多B.喜欢足球的人数(1)班比(2)班多
C.喜欢羽毛球的人数(1)班比(2)班多D.喜欢篮球的人数(2)班比(1)班多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AB上,以AD为直径的⊙O与边BC相切于点E,与边AC相交于点G,且![]() ,连接GO并延长交⊙O于点F,连接BF.
,连接GO并延长交⊙O于点F,连接BF.
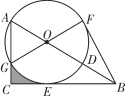
(1)求证:AO=AG;
(2)求证:BF是⊙O的切线;
(3)若BD=6,求图形中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
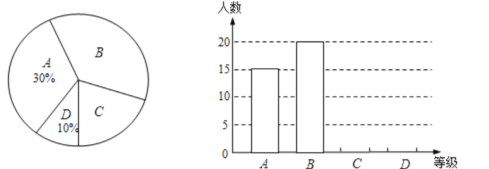
⑴ 九年级(1)班参加体育测试的学生有_________人;
⑵ 将条形统计图补充完整;
⑶ 在扇形统计图中,等级B部分所占的百分比是___,等级C对应的圆心角的度数为___°;
⑷ 若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有___人.
查看答案和解析>>
科目:初中数学 来源: 题型:
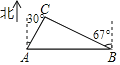
【题目】如图,从A城市到B城市要翻过一座大山,现需要打通隧道,修建高铁方便两地出行,已知在A城市的北偏东30°方向和B城市的北偏西67°方向有一C地,A,C相距230km,求A,B两个城市之间的距离.(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.7,结果精确到1km)
≈1.7,结果精确到1km)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标![]() 系中,直线
系中,直线![]() 与坐标轴
与坐标轴![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() 过
过![]() 两点的抛物线
两点的抛物线![]() ,点
,点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() 交抛物线于点
交抛物线于点![]() .
.
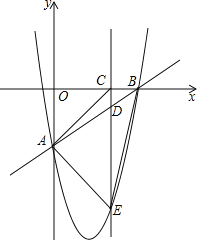
(1)求抛物线的解析式;
(2)当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(3)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数![]() (
(![]() )的图像交于B(m,4)
)的图像交于B(m,4)

(1)求![]() 的值;
的值;
(2)以AB为一边,在AB的左侧作正方形![]() ,求C点坐标;
,求C点坐标;
(3)将正方形![]() 沿着
沿着![]() 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形![]() ,线段
,线段![]() 的中点为点
的中点为点![]() ,若点
,若点![]() 和点
和点![]() 同时落在反比例函数
同时落在反比例函数![]() 的图像上,求n的值.
的图像上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
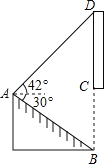
【题目】2021年世界园艺博览会将在扬州枣林湾举办,有一块枣林湾博览会的直传牌CD竖立在路边,其中CB是支柱.小梅同学想计算出CD的长度.于是在A处测得支柱B处的俯角为30°.测得顶端D处的仰角为42°,同时测量出AB的长度是10m,BC的长度是6m.求宜传牌CD的长度(结果保留小数点后一位).(参考数据:![]() ≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com