
分析 (1)根据关于x的一元二次方程2x2-4mx+2m2+3m-2=0有两个实数根,得出b2-4ac≥0,然后代入求解即可;
(2)根据根与系数的关系得x1+x2=2m,x1•x2=$\frac{1}{2}$(2m2+3m-2),再把x12+x22进行变形,即可得出x12+x22=2(m-$\frac{3}{4}$)2+$\frac{7}{8}$,再根据二次函数的性质和(1)中的m的取值即可得出答案.
解答 解:(1)∵一元二次方程2x2-4mx+2m2+3m-2=0有两个实数根,
∴b2-4ac=(-4m)2-4×2(2m2+3m-2)≥0,
∴-24m+16≥0,
∴m≤$\frac{2}{3}$,
∴实数m的取值范围为≤$\frac{2}{3}$;
(2)∵x1+x2=2m,x1•x2=$\frac{1}{2}$(2m2+3m-2),
∴x12+x22=(x1+x2)2-2x1x2=(2m)2-2×$\frac{1}{2}$(2m2+3m-2)=2m2-3m+2=2(m-$\frac{3}{4}$)2+$\frac{7}{8}$,
∵m≤$\frac{2}{3}$,$\frac{2}{3}$<$\frac{3}{4}$,
∴当x=$\frac{2}{3}$时,x12+x22=2($\frac{2}{3}$-$\frac{3}{4}$)2+$\frac{7}{8}$=$\frac{8}{9}$,
∴当x=$\frac{2}{3}$时,m有最小值,最小值是$\frac{8}{9}$.
点评 本题考查了根的判别式、根与系数的关系与二次函数的最值问题,一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


科目:初中数学 来源: 题型:解答题
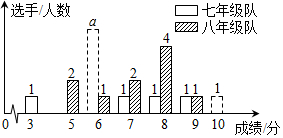
| 队别 | 平均分 | 众数 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | a | m | 3.41 | 90% | 20% |
| 八年级 | 7.1 | p | q | 1.69 | 80% | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
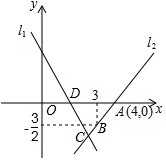 如图,直线l1的表达式为y=-3x+3,与x轴交于点D,过点A、B两点的直线l2:y=$\frac{3}{2}$x-6与直线l1交于点C,则△ADC的面积为$\frac{9}{2}$.
如图,直线l1的表达式为y=-3x+3,与x轴交于点D,过点A、B两点的直线l2:y=$\frac{3}{2}$x-6与直线l1交于点C,则△ADC的面积为$\frac{9}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com