①②③④⑤
分析:根据等腰三角形三线合一的性质,角平分线上的点到角的两边的距离相等,线段垂直平分线上的点到线段两端点的距离相等判断出①②③正确,然后利用“HL”证明Rt△BDE和Rt△CDF全等,根据全等三角形对应角相等可得∠BDE=∠CDF,全等三角形对应边相等可得BE=CF,然后求出AE=AF,从而最后得解.
解答:∵AD平分∠BAC,
∴AD上任意一点到AB、AC两边的距离相等(角平分线上的点到角的两边的距离相等),故①正确;
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,且BD=CD,故③正确,
∴AD上任意一点到B、C两点的距离相等(线段垂直平分线上的点到线段两端点的距离相等),故②正确;
∵DE⊥AB于E,DF⊥AC,
∴∠BED=∠CFD=90°,
在Rt△BDE和Rt△CDF中,
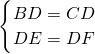
,
∴Rt△BDE≌Rt△CDF(HL),
∴∠BDE=∠CDF,故④正确;
BE=CF,
∴AB-BE=AC-CF,
即AE=AF,故⑤正确,
综上所述,正确的有①②③④⑤.
故答案为:①②③④⑤.
点评:本题考查了等腰三角形三线合一的性质,全等三角形的判定与性质,角平分线上的点到角的两边的距离相等,线段垂直平分线上的点到线段两端点的距离相等的性质,综合题,但难度不大,熟记各性质是解题的关键.

 如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,则下列五个结论:
如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,则下列五个结论: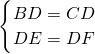 ,
,

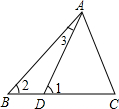 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.