
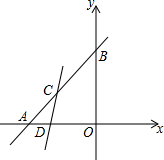
 如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1
如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1分析 (1)由三角形AOB为等腰直角三角形,且面积为18,求出OA与OB的长,确定出A与B的坐标,即可确定出直线AB解析式;
(2)由C为AB的中点,根据A与B坐标,利用中点坐标公式求出C坐标即可;
(3)根据直线l分三角形AOB面积为5:1,求出三角形ACD面积,以AD为底边,C纵坐标为高求出AD的长,确定出D坐标,进而求出直线l方程即可.
解答 解:(1)∵S△AOB=18,且△AOB为等腰直角三角形,
∴OA=OB=6,即A(-6,0),B(0,6),
设直线AB解析式为y=kx+b,
把A与B坐标代入得:$\left\{\begin{array}{l}{-6k+b=0}\\{b=6}\end{array}\right.$,
解得:k=1,b=6,
则直线AB解析式为y=x+6;
(2)∵C为AB的中点,A(-6,0),B(0,6),
∴C(-3,3);
(3)∵过点C的直线l把△AOB面积分成5:1,S△AOB=18,
∴S△ACD=$\frac{5}{6}$×18=15或S△ACD=$\frac{1}{6}$×18=3,
设D坐标为(d,0)d<0,
若△ACD面积为3时,C纵坐标为3,AD=|d-6|,
∵S△ACD=$\frac{1}{2}$•|d-6|•3=3,
∴|d-6|=2,即d-6=2或-2,
解得:d=8(舍去)或d=4(舍去);
若△ACD面积为15时,C纵坐标为3,AD=|d-6|,
∵S△ACD=$\frac{1}{2}$•|d-6|•3=15,
∴|d-6|=10,即d-6=10或-10,
解得:d=16(舍去)或d=-4,
此时D(0,-4),
设直线CD解析式为y=px+q,
把C与D坐标代入得:$\left\{\begin{array}{l}{-3p+q=3}\\{q=-4}\end{array}\right.$,
解得:p=-$\frac{7}{3}$,q=-4,
则直线l解析式为y=-$\frac{7}{3}$x-4.
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,待定系数法求一次函数解析式,等腰直角三角形的性质,熟练掌握待定系数法是解本题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:填空题
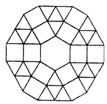 如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.
如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 把正整数1,2,3,…,按如图所示排列.第1行第1列的数为1,第1行第2列的数为2,第1行第3列的数为6,那么第1行第100列的数为4951.
把正整数1,2,3,…,按如图所示排列.第1行第1列的数为1,第1行第2列的数为2,第1行第3列的数为6,那么第1行第100列的数为4951.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
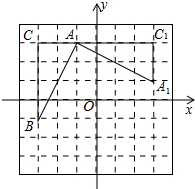 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )| A. | (0,0) | B. | (-1,0) | C. | (1,0) | D. | (0,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
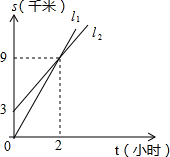 A、B两人相距3千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知A的速度比B快,请根据图象进行判断:
A、B两人相距3千米,他们同时朝同一目的地匀速直行,并同时到达目的地,已知A的速度比B快,请根据图象进行判断:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com