
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
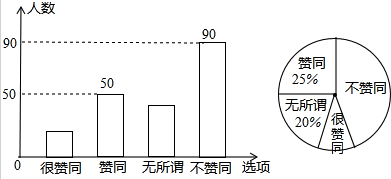
分析 (1)根据表示赞同的人数是50,所占的百分比是25%即可求得总人数;
(2)利用360°乘以对应的百分比即可求得圆心角的度数;
(3)利用总人数乘以对应的百分比即可求解;
(4)求得表示很赞同的人数,然后利用概率公式求解.
解答 解:(1)接受这次调查的家长人数为:50÷25%=200(人),故命题正确;
(2)“不赞同”的家长部分所对应的扇形圆心角大小是:360×$\frac{90}{200}$=162°,故命题正确;
(3)表示“无所谓”的家长人数为200×20%=40(人),故命题正确;
(4)表示很赞同的人数是:200-50-40-90=20(人),
则随机抽查一名接受调查的家长,恰好抽到“很赞同”的家长的概率是$\frac{20}{200}$=$\frac{1}{10}$,故命题正确.
故选A.
点评 本题考查的是条形统计图和扇形统计图的综合运用,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.用到的知识点为:概率=所求情况数与总情况数之比.总体数目=部分数目÷相应百分比.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
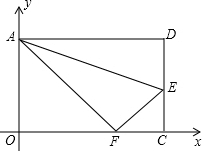 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为(10,3).
如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为(10,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-3}$ | B. | $\sqrt{0}$ | C. | $\sqrt{2}$ | D. | $\sqrt{(-1)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com