
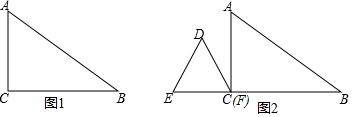
���� ��1�������ù��ɶ������a������һԪ���η��̵Ľ����m��
��2����������������������ε������ʽ�������������ε������ɵó����ۣ�
��3�����жϳ���BDM�ס�BAC����DM����������⼴�ɣ�
��� �⣺��1����Rt��ABC�У���C=90�㣬AB=5cm��BC=a cm��AC=3cm��
���ݹ��ɶ����ɵã�BC=4cm����a=4��
��a�Ƿ���x2-��m-1��x+m+4=0�ĸ�
��42-��m-1����4+m+4=0�ĸ���
��m=8��
��2���ɣ�1����a=4����ȱ�������DEF�ı߳�Ϊ$\frac{a}{2}$=2��cm����
��ͼ��1����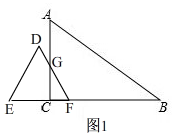
��0��x��1ʱ����֪��DFC=60�㣬
�ߡ�ACF=90�㣬
���CGF=30�㣬
��CG=$\sqrt{3}$CF=$\sqrt{3}$x
��y=S��CGF=$\frac{1}{2}$CF•CG=$\frac{1}{2}$x•$\sqrt{3}$x=$\frac{\sqrt{3}}{2}$x2��
��ͼ��2����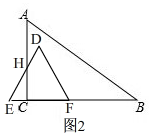
��1��x��2ʱ��BE=2-x��HC=$\sqrt{3}$EC=$\sqrt{3}$��2-x����
��S��HEC=$\frac{1}{2}$EC•HC=$\frac{1}{2}$��2-x��•$\sqrt{3}$��2-x��=$\frac{\sqrt{3}}{2}$��2-x��2��
��y=S��DEF-S��HEC=$\frac{\sqrt{3}}{4}$��22-$\frac{\sqrt{3}}{2}$��2-x��2=-$\frac{\sqrt{3}}{2}$x2+2$\sqrt{3}$x-$\sqrt{3}$
���ϣ�$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}^{2}��0��x��1��}\\{-\frac{\sqrt{3}}{2}{x}^{2}+2\sqrt{3}x-\sqrt{3}��1��x��2��}\end{array}\right.$
��3����ͼ��3����
����D���߶�AB�ϣ�
����D��DM��BC�ڵ�M����ʱDM��AC��
���BDM�ס�BAC
��$\frac{BM}{BC}=\frac{DM}{AC}$��$\frac{4-x+1}{4}=\frac{DM}{3}$��
��DM=$\frac{15-3x}{4}$
�ֵȱ�������DEF�ı߳�2��
��DM=$\sqrt{3}$
��$\frac{15-3x}{4}=\sqrt{3}$��
��x=$\frac{15-4\sqrt{3}}{3}$
��������$\frac{15-4\sqrt{3}}{3}$ sʱ����D���߶�AB�ϣ�
���� �������������ۺ��⣬��Ҫ�����˹��ɶ�����һԪ���η��̵Ľ⣬�����ε������ʽ�����������ε��ж��������ʣ��⣨1���Ĺؼ������a��ֵ���⣨2���Ĺؼ��Ƿ�������ۣ��⣨3���Ĺؼ����жϳ���BDM�ס�BAC����һ���е��Ѷȵ��п������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
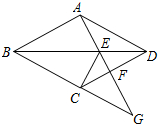 ��ͼ���ı���ABCD�����Σ���G��BC�ӳ�����һ�㣬����AG���ֱ�BD��CD�ڵ�E��F������CE��
��ͼ���ı���ABCD�����Σ���G��BC�ӳ�����һ�㣬����AG���ֱ�BD��CD�ڵ�E��F������CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
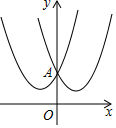 ����������κ�����ͼ�����y��Գƣ����Ǿͳ����������κ�����Ϊ������y��Գƶ��κ���������ͼ��ʾ���κ���y1=x2+2x+2��y2=x2-2x+2�ǡ�����y��Գƶ��κ�������
����������κ�����ͼ�����y��Գƣ����Ǿͳ����������κ�����Ϊ������y��Գƶ��κ���������ͼ��ʾ���κ���y1=x2+2x+2��y2=x2-2x+2�ǡ�����y��Գƶ��κ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���⣺���������ĸ߶� | ||
| ��������� | �������� | |
| ͼʾ | 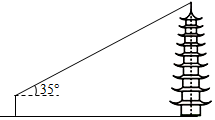 | 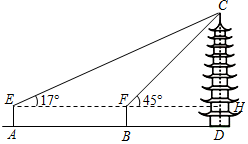 |
| ����������������� | �� �þ������߶�Ϊ1.6m�IJ��������������˵�����Ϊ35�㣬����Ƥ�߲�ò��������λ��������ײ���Ե����̾���Ϊ30m�� | �ڵ�A�þ������߶�Ϊ1.6m�IJ��������������˵�����Ϊ17�㣬Ȼ����AD������58.8m�����B������������˵�����Ϊ45�㣮 |
| ����� | sin35���0.57��cos35���0.82��tan35���0.70 | sin17���0.29��cos17���0.96��tan17���0.30��$\sqrt{2}$��1.41 |
| ��������߶� �������ȷ��0.1m�� | 30��tan35��+1.6��22.6��m�� | |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
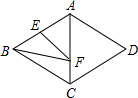 ��ͼ������ABCD�ı߳�Ϊ4����BAD=120�㣬��E��AB���е㣬��F��AC�ϵ�һ���㣬��EF+BF����Сֵ�ǣ�������
��ͼ������ABCD�ı߳�Ϊ4����BAD=120�㣬��E��AB���е㣬��F��AC�ϵ�һ���㣬��EF+BF����Сֵ�ǣ�������| A�� | 4 | B�� | 2$\sqrt{3}$ | C�� | 4$\sqrt{3}$ | D�� | 2$\sqrt{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com