
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
【答案】(1)50°或20°或80°(2)当0<x<90且x≠60时,∠B有三个不同的度数
【解析】
(1)由于等腰三角形的顶角和底角没有明确,因此要分类讨论;
(2)分两种情况:①90≤x<180;②0<x<90,结合三角形内角和定理求解即可.
(1)若∠A为顶角,则∠B=(180°-∠A)÷2=50°;
若∠A为底角,∠B为顶角,则∠B=180°-2×80°=20°;
若∠A为底角,∠B为底角,则∠B=80°.
故∠B=50°或20°或80°.
(2)分两种情况:
①当90≤x<180时,∠A只能为顶角,
则∠B的度数只有一个;
②当0<x<90时,
若∠A为顶角,则∠B=![]() °;
°;
若∠A为底角,∠B为顶角,则∠B=(180-2x)°;
若∠A为底角,∠B为底角,则∠B=x°.
当![]() ≠180-2x且180-2x≠x且
≠180-2x且180-2x≠x且![]() ≠x,
≠x,
即x≠60时,∠B有三个不同的度数.
综上所述,当0<x<90且x≠60时,∠B有三个不同的度数.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向向右平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 . 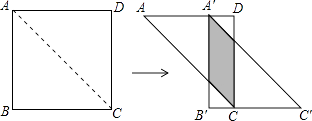
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.

(1)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.
(2)若DC=2,求证:△ABD≌△DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月13日,周杰伦2017“地表最强”世界巡回演唱会在奥体中心盛大举行,1号巡逻员从舞台走往看台,2号巡逻号从看台走往舞台,两人同时出发,分别以各自的速度在舞台与看台间匀速走动,出发1分钟后,1号巡逻员发现对讲机遗忘在出发地,便立即返回出发地,拿到对讲机后(取对讲机时间不计)立即再从舞台走往看台,结果1号巡逻员先到达看台,2号巡逻员继续走到舞台,设2号巡逻员的行驶时间为x(min),两人之间的距离为y(m),y与x的函数图象如图所示,则当1号巡逻员到达看台时,2号巡逻员离舞台的距离是米.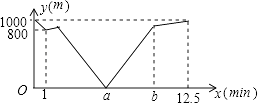
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品经销店欲购进A、B两种纪念品,用160元购进的A种纪念品与用240元购进的B种纪念品的数量相同,每件B种纪念品的进价比A种纪念品的进价贵10元.
(1)求A、B两种纪念品每件的进价分别为多少元?
(2)若该商店A种纪念品每件售价24元,B种纪念品每件售价35元,这两种纪念品共购进1 000件,这两种纪念品全部售出后总获利不低于4 900元,求A种纪念品最多购进多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在相同条件下各射靶10次,甲10次射靶的成绩的情况如图所示,乙10次射靶的成绩依次是:3环、4环、5环、8环、7环、7环、8环、9环、9环、10环.
(1)请在图中画出乙的射靶成绩的折线图;
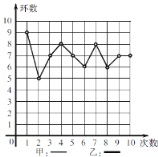
(2) 请从下列两个不同角度对这次测试结果进行分析.
①从平均数和方差相结合看(分析谁的成绩稳定些);
②从平均数和中位数相结合看(分析谁的成绩好些).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC.过AB,DC的中点E,F作直线,直线EF与直线AD,BC分别相交于点M,N.
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可得∠AMF与∠ENB有何数量关系?(不需证明).
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠ENB有何数量关系?请分别写出猜想,并任选一种情况证明.
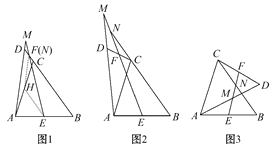
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com