
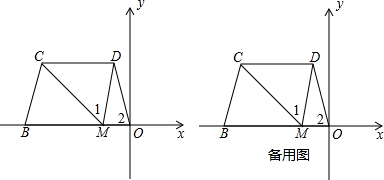
分析 (1)首先根据等腰梯形的性质,判断出∠MBC=∠DOM;然后根据∠1=∠2以及三角形外角的性质,判断出∠BMC=∠ODM;最后根据三角形相似的判定方法,判断出△BMC∽△ODM即可.
(2)根据△BMC∽△ODM,可得$\frac{BM}{OD}=\frac{BC}{OM}$,所以$\frac{5-OM}{2}=\frac{2}{OM}$,据此求出OM的长度,即可确定出点M的坐标.
(3)首先根据题意,可得∠DME=∠CMF=a;然后根据△BMC∽△ODM,可得∠BCM=∠OMD,再根据CD∥BO,推得∠EDM=∠FCM,据此判断出△DME∽△CMF即可.
解答 (1)证明:如图1, ,
,
∵四边形OBCD为等腰梯形,
∴∠MBC=∠DOM,
∵∠DMB=∠1+∠BMC=∠ODM+∠2,∠1=∠2,
∴∠BMC=∠ODM,
在△BMC和△ODM中,
$\left\{\begin{array}{l}{∠MBC=∠DOM}\\{∠BMC=∠ODM}\end{array}\right.$
∴△BMC∽△ODM.
(2)解:由(1)知△BMC∽△ODM,
∴$\frac{BM}{OD}=\frac{BC}{OM}$,
∵OD=BC=2,OB=5,
∴$\frac{5-OM}{2}=\frac{2}{OM}$,
整理,可得
OM2-5OM+4=0,
解得OM=1或OM=4,
∴点M的坐标为(-1,0)或(-4,0).
(3)解:△DME与△CMF相似.
如图2, ,
,
根据题意,可得∠DME=∠CMF=a,
由(1)知△BMC∽△ODM,
∴∠BCM=∠OMD,
又∵CD∥BO,
∴∠EDM=∠OMD,
∴∠EDM=∠BCM,
即∠EDM=∠FCM,
在△DME和△CMF中,
$\left\{\begin{array}{l}{∠DME=∠CMF}\\{∠EDM=∠FCM}\end{array}\right.$
∴△DME∽△CMF.
点评 (1)此题主要考查了相似形综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
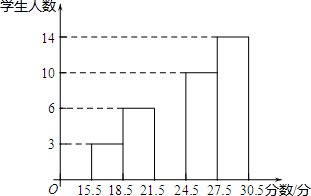 某学校为了了解800名初中毕业生体育考试成绩的情况(满分30分,得分为整数),从中随机抽取了部分学生的体育考试成绩,制成如下图所示的频数分布直方图.已知成绩在18.5~21.5这一组的频率为0.12,请回答下列问题:
某学校为了了解800名初中毕业生体育考试成绩的情况(满分30分,得分为整数),从中随机抽取了部分学生的体育考试成绩,制成如下图所示的频数分布直方图.已知成绩在18.5~21.5这一组的频率为0.12,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
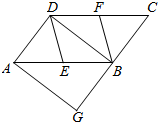 如图,在?ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作平行四边形AGDB交CB的延长线于点G.
如图,在?ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作平行四边形AGDB交CB的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-3x-1 | B. | -$\frac{7}{3}$x2y3 | C. | $\frac{2xy}{m}$ | D. | $\frac{1}{2}$(x2-y) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com