已知:二次函数y=(n-1)x2+2mx+1图象的顶点在x轴上.
(1)试判断这个二次函数图象的开口方向,并说明你的理由;
(2)求证:函数y=m2x2+2(n-1)x-1的图象与x轴必有两个不同的交点;
(3)如果函数y=m2x2+2(n-1)x-1的图象与x轴相交于点A(x1,0)、B(x2,0),与y轴相交于点C,且△ABC的面积等于2.求这个函数的解析式?
分析:(1)本题需根据二次函数图象的顶点在x轴上得出4m2-4(n-1)=0,从而得出n-1>0,证出抛物线开口向上.
(2)本题需先求出△的值,再证明△>0即可得出函数的图象与x轴必有两个交点.
(3)本题需根据根与系数的关系列出式子,求出AB的长,列出方程求m2与n即可求出这个函数的解析式.
解答:(1)∵二次函数y=(n-1)x
2+2mx+1图象的顶点在x轴上,
∴n-1≠0,△=4m
2-4(n-1)=0.
∴m
2=n-1≠0.
又∵m
2≥0,∴n-1>0.
∴这个函数图象的开口方向向上.
(2)∵m
2≠0,
∴这个函数是二次函数.△=4(n-1)
2+4m
2.
∵m
2=n-1≠0,∴(n-1)
2>0,m
2>0.
∴△>0.
∴函数y=m
2x
2+2(n-1)x-1的图象与x轴必有两个不同的交点.
(3)由题意,得
x1+x2=-,
x1x2=-.
∵m
2=n-1,∴
x1+x2=-=-2.
而AB=|x
1-x
2|,点C的坐标为(0,-1).
∴
|x1-x2|×1=2.
∴|x
1-x
2|=4.
∴
(x1-x2)2=(x1+x2)2-4x1x2=(-2)2+=16.
∴
m2=.
∴
n-1=.
∴所求的函数解析式为
y=x2+x-1.
点评:本题主要考查了二次函数的图象与x轴的交点,在解题时要能根据二次函数的图象与x轴的交点列出式子求出答案是本题的关键.



 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.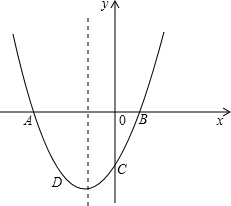 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.