
已知直线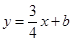 与抛物线
与抛物线 交于点A(1,
交于点A(1,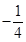 ),与
),与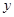 轴交于点C.
轴交于点C.
(1)求抛物线的解析式和点C的坐标;
(2)把(1)中的抛物线向右平移2个单位,再向上平移 个单位(
个单位( >0),抛物线与
>0),抛物线与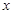 轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求
轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求 的值;
的值;
(3)如图,把抛物线向右平移2个单位,再向上平移 个单位(
个单位( >0),抛物线与
>0),抛物线与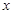 轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时
轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)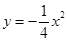 ,C(0,-1);(2)
,C(0,-1);(2) ;(3)最小值为
;(3)最小值为 ,
,
解析试题分析:(1)把A(1,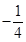 )分别代入直线
)分别代入直线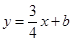 与抛物线
与抛物线 ,即可求得结果;
,即可求得结果;
(2)先根据平移的特征得到平移后的函数关系式,再根据直径所对的圆周角是直角即可得到结果;
(3)先设出平移后抛物线的解析式,不难得出平移后抛物线的对称轴.因此过C、P、Q三点的圆的圆心必在对称轴上,要使圆的面积最小,那么圆心到C点的距离也要最小,即两点的纵坐标相同,即可得到圆的半径,求出圆心的坐标.可设出平移后的抛物线的解析式,表示出PQ的长,如果设对称轴与x轴的交点为E,那么可表示出PE的长,根据勾股定理即可确定平移的距离.
(1)把A(1,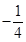 )分别代入直线
)分别代入直线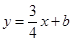 与抛物线
与抛物线 ,
,
可得 ,
,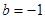 ,
,
∴抛物线的解析式为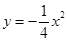 ,直线的解析式为,
,直线的解析式为,
在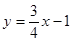 中,当
中,当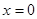 时,
时, ,
,
∴C的坐标为(0,-1);
(2)设平移后的抛物线函数关系式为 ,
,
由题意得,此时抛物线的图象经过原点(0,0),
则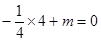 ,解得
,解得 ;
;
(3)设平移后的抛物线函数关系式为 ,
,
令 ,则
,则 ,
,
∵过C、P、Q三点的圆的圆心一定在直线x=2上,点C为定点,
∴要使圆的面积最小,圆的半径应等于点C到直线x=2的距离,此时,半径为2,面积为 ,
,
设圆心为O,PQ的中点为E,连接OE,OP.
在三角形CEM中,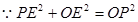 ,
, ,解得
,解得 ,
,
∴当 时,过C、P、Q三点的圆的面积最小,最小面积为
时,过C、P、Q三点的圆的面积最小,最小面积为 .
.
考点:本题考查的是二次函数的综合题
点评:解答本题的关键是注意平移不改变二次项的系数;抛物线的平移,看顶点的平移即可;左右平移,只改变顶点的横坐标,左减右加;上下平移,只改变顶点的纵坐标,上加下减.


科目:初中数学 来源: 题型:
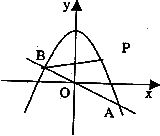
如图,已知直线![]() 与抛物线
与抛物线![]() 交于A、B两点.
交于A、B两点.
(1)求A、B两点的坐标;
(2)求线段AB的垂直平分线的解析式;
(3)如图,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.

查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江建德李家镇初级中学九年级上期中考试数学试卷(解析版) 题型:解答题
已知直线 与抛物线
与抛物线 交于点A(1,
交于点A(1, ),与
),与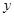 轴交于点C.
轴交于点C.
(1)求抛物线的解析式和点C的坐标;
(2)把(1)中的抛物线向右平移2个单位,再向上平移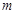 个单位(
个单位(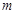 >0),抛物线与
>0),抛物线与 轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求
轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求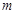 的值;
的值;
(3)如图,把抛物线向右平移2个单位,再向上平移 个单位(
个单位( >0),抛物线与
>0),抛物线与 轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时
轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知直线
如图所示,已知直线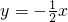 与抛物线
与抛物线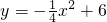 交于A、B两点,点C是抛物线的顶点.
交于A、B两点,点C是抛物线的顶点.查看答案和解析>>
科目:初中数学 来源:2010-2011学年重庆市九龙坡区陶家中学九年级(上)第三次月考数学试卷(解析版) 题型:解答题
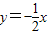 与抛物线
与抛物线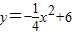 交于A、B两点,点C是抛物线的顶点.
交于A、B两点,点C是抛物线的顶点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com