
分析 设点A的坐标为(-$\frac{6}{a}$,a),根据点B的坐标为(4,0),△AOB的面积为6,列方程即可得到结论.
解答 解:设点A的坐标为(-$\frac{6}{a}$,a),
∵点B的坐标为(4,0).若△AOB的面积为6,
∴S△AOB=$\frac{1}{2}$4×|a|=6,
解得:a=±3,
∴点A的坐标为(-2,3),(2,-3).
故答案为:(-2,3),(2,-3).
点评 本题考查了反比例函数系数k的几何意义,三角形的面积的计算,在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{|k|}{2}$,且保持不变.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
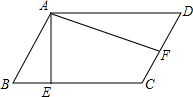 如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )
如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
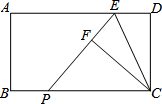 如图,在矩形ABCD中,点E是AD上的点,且tan∠ECD=$\frac{1}{2}$,将△CDE沿CE对折,得到△CEF,延长EF交于BC点P,则sin∠EPC=$\frac{4}{5}$.
如图,在矩形ABCD中,点E是AD上的点,且tan∠ECD=$\frac{1}{2}$,将△CDE沿CE对折,得到△CEF,延长EF交于BC点P,则sin∠EPC=$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王杰为了测量他家小楼附近楼房AB的高度,他从楼底的B处测得到他家小楼顶部D的仰角∠CBD为30°,又测得两幢楼之间的距离BC为10$\sqrt{3}$m.(以下计算结果精确到0.1m,参考值$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
王杰为了测量他家小楼附近楼房AB的高度,他从楼底的B处测得到他家小楼顶部D的仰角∠CBD为30°,又测得两幢楼之间的距离BC为10$\sqrt{3}$m.(以下计算结果精确到0.1m,参考值$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.
如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com