
【题目】如图,在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,CD⊥AD于点D,点E,A,D在同一直线上,且∠ACD=35°,求∠BAE的度数.

【答案】59°
【解析】
设∠BAC为3x度,∠BCA为2x度,在△BAC中,利用三角形内角和定理求得∠BAC和∠DAC,在△ACD中利用三个角的和定理求∠DAC,因为∠EAD为平角,用180°-∠DAC-∠BAC即可得∠BAE的度数.
在△ABC中,
因为∠BAC∶∠BCA=3∶2,
所以可设∠BAC=3x°,∠BCA=2x°.
因为∠B+∠BAC+∠BCA=180°,∠B=70°,
所以70+3x+2x=180,所以x=22,
所以∠BAC=3×22°=66°.
又因为CD⊥AD,
所以∠D=90°,
所以∠CAD+∠ACD=90°,
所以∠CAD=90°-∠ACD=90°-35°=55°.
因为∠DAE是平角,
所以∠BAE=180°-∠BAC-∠CAD=180°-66°-55°=59°.


科目:初中数学 来源: 题型:
【题目】(8分)自2014年12月启动“绿茵行动,青春聚力”郴州共青林植树活动以来,某单位筹集7000元购买了桂花树和樱花树共30棵,其中购买桂花树花费3000元.已知桂花树比樱花树的单价高50%,求樱花树的单价及棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
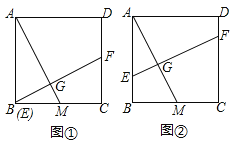
【题目】如图,正方形ABCD,AB=4,点M是边BC的中点,点E是边AB上的一个动点,作EG⊥AM交AM于点G,EG的延长线交线段CD于点F.
(1)如图①,当点E与点B重合时,求证:BM=CF;
(2)设BE=x,梯形AEFD的面积为y,求y与x的函数解析式,并写出定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“马航事件”的发生引起了我国政府的高度重视,迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机观测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为45°的方向上,请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值: ![]() ≈1.7)
≈1.7)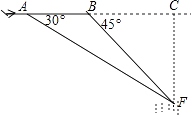
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,点B是数轴上原点O两侧的两点,其中点A在负半轴上,且满足AB=12,OB=2OA.
(1)点A,B在数轴上对应的数分别为 和 ;
(2)点A,B同时分别以每秒2个单位长度和每秒4个单位长度的速度向左运动.
①经过几秒后,OA=3OB;
②点A,B在运动的同时,点P以每秒2个单位长度的速度从原点向右运动,经过几秒后,点A,B,P中的某一点成为其余两点所连线段的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )

A. 14cm B. 17cm C. 20cm D. 23cm
查看答案和解析>>
科目:初中数学 来源: 题型:
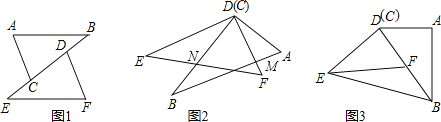
【题目】如图1所示,已知在△ABC和△DEF中,AB=EF,∠B=∠E,EC=BD
(1)试说明:△ABC≌△FED;
(2)若图形经过平移和旋转后得到图2,且有∠EDB=25°,∠A=66°,试求∠AMD的度数;
(3)将图形继续旋转后得到图3,此时D,B,F三点在同一条直线上,若DB=2DF,连接EB,已知△EFB的面积为5cm2,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;
②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线. 其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com