
【题目】抛物线![]() 经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求此抛物线的解析式;
(2)已知点D![]() 在第四象限的抛物线上,求点D关于直线BC对称的点D’的坐标;
在第四象限的抛物线上,求点D关于直线BC对称的点D’的坐标;
(3)在(2)的条件下,连结BD,问在x轴上是否存在点P,使![]() ,若存在,请求出P点的坐标;若不存在,请说明理由.
,若存在,请求出P点的坐标;若不存在,请说明理由.
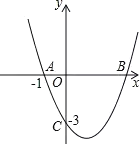
【答案】(1)![]()
(2)(0,-1)
(3)(1,0)(9,0)
【解析】
(1)将A(1,0)、C(0,3)两点坐标代入抛物线y=ax2+bx3a中,列方程组求a、b的值即可;
(2)将点D(m,m1)代入(1)中的抛物线解析式,求m的值,再根据对称性求点D关于直线BC对称的点D'的坐标;
(3)分两种情形①过点C作CP∥BD,交x轴于P,则∠PCB=∠CBD,②连接BD′,过点C作CP′∥BD′,交x轴于P′,分别求出直线CP和直线CP′的解析式即可解决问题.
解:(1)将A(1,0)、C(0,3)代入抛物线y=ax2+bx3a中,
得![]() ,
,
解得![]()
∴y=x22x3;
(2)将点D(m,m1)代入y=x22x3中,得
m22m3=m1,
解得m=2或1,
∵点D(m,m1)在第四象限,
∴D(2,3),
∵直线BC解析式为y=x3,
∴∠BCD=∠BCO=45°,CD′=CD=2,OD′=32=1,
∴点D关于直线BC对称的点D'(0,1);
(3)存在.满足条件的点P有两个.
①过点C作CP∥BD,交x轴于P,则∠PCB=∠CBD,
∵直线BD解析式为y=3x9,
∵直线CP过点C,
∴直线CP的解析式为y=3x3,
∴点P坐标(1,0),
②连接BD′,过点C作CP′∥BD′,交x轴于P′,
∴∠P′CB=∠D′BC,
根据对称性可知∠D′BC=∠CBD,
∴∠P′CB=∠CBD,
∵直线BD′的解析式为![]()
∵直线CP′过点C,
∴直线CP′解析式为![]() ,
,
∴P′坐标为(9,0),
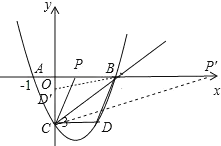
综上所述,满足条件的点P坐标为(1,0)或(9,0).


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】“康河泛舟,问道剑桥”,甲乙两人相约泛舟康河,路线均为从![]() 到
到![]() 再返回
再返回![]() ,且
,且![]() 全长2千米,甲出发2分钟后,乙以另一速度出发,结果同时到达目的
全长2千米,甲出发2分钟后,乙以另一速度出发,结果同时到达目的![]() 地,甲到达目的地拍照5分钟便原速返回
地,甲到达目的地拍照5分钟便原速返回![]() 地;乙到达
地;乙到达![]() 地后休息了2分钟,然后立即提速为原速的
地后休息了2分钟,然后立即提速为原速的![]() 倍返回
倍返回![]() 地.甲乙之间的距离
地.甲乙之间的距离![]() (单位:米)与甲的行驶时间
(单位:米)与甲的行驶时间![]() (单位:分钟)之间的函数关系如图所示.则当乙回到
(单位:分钟)之间的函数关系如图所示.则当乙回到![]() 地时,甲距离
地时,甲距离![]() 地________米.
地________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解九年级A、B两个班级学生的跳绳成绩情况,在每个班各随机抽取20名同学(不分性别)测试每分钟跳绳次数,收集数据后制作成如下的统计图.

(1)已知一分钟跳绳次数在175次及以上的为成绩优秀,两个班的人数均为50人,请你估计一下,哪个班级优秀人数多?多几人?
(2)请你选择适当的统计量来说明哪个班级的整体成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十一”购物街中,某儿童品牌玩具专卖店购进了![]() 两种玩具,其中
两种玩具,其中![]() 类玩具的金价比
类玩具的金价比![]() 玩具的进价每个多
玩具的进价每个多![]() 元.经调查发现:用
元.经调查发现:用![]() 元购进
元购进![]() 类玩具的数量与用
类玩具的数量与用![]() 元购进
元购进![]() 类玩具的数量相同.
类玩具的数量相同.
(1)求![]() 的进价分别是每个多少元?
的进价分别是每个多少元?
(2)该玩具店共购进![]() 了两类玩具共
了两类玩具共![]() 个,若玩具店将每个
个,若玩具店将每个![]() 类玩具定价为
类玩具定价为![]() 元出售,每个
元出售,每个![]() 类玩具定价
类玩具定价![]() 元出售,且全部售出后所获得的利润不少于
元出售,且全部售出后所获得的利润不少于![]() 元,则该淘宝专卖店至少购进
元,则该淘宝专卖店至少购进![]() 类玩具多少个?
类玩具多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,已知点A(﹣3,﹣3),点B(﹣1,﹣3),点C(﹣1,﹣1).
(1)画出△ABC;
(2)画出△ABC关于x轴对称的△A1B1C1,并写出A1点的坐标: ;
(3)以O为位似中心,在第一象限内把△ABC扩大到原来的两倍,得到△A2B2C2,并写出A2点的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
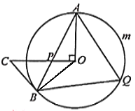
【题目】如图,AB是⊙O的弦,过点O作OC⊥OA,OC交于AB于P,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)已知∠BAO=25°,点Q是弧AmB上的一点.
①求∠AQB的度数;
②若OA=18,求弧AmB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com