
分析 (1)方程变形后,利用平方根定义开方即可求出解;
(2)方程利用公式法求出解即可.
解答 解:(1)方程整理得:(x+3)2=4,
开方得:x+3=±2,即x+3=2或x+3=-2,
解得:x1=-1,x2=-5;
(2)这里a=2,b=-4,c=-1,
∵△=b2-4ac=(-4)2-4×2×(-1)=24>0,
∴x=$\frac{{-b±\sqrt{{b^2}-4ac}}}{2a}$=$\frac{{-(-4)±\sqrt{24}}}{2×2}$=$\frac{{4±2\sqrt{6}}}{4}$=$\frac{{2±\sqrt{6}}}{2}$,
解得:x1=$\frac{{2+\sqrt{6}}}{2}$,x2=$\frac{{2-\sqrt{6}}}{2}$.
点评 此题考查了解一元二次方程-公式法,以及直接开平方法,熟练掌握各种解法是解本题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:填空题
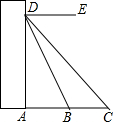 如图,小明家所在住宅楼楼前广场的宽AB为30米,线段BC为AB正前方的一条道路的宽.小明站在家里点D处观察B,C两点的俯角分别为60°和45°,已知DA垂直地面,则这条道路的宽BC为21.96米($\sqrt{3}$≈1.732)
如图,小明家所在住宅楼楼前广场的宽AB为30米,线段BC为AB正前方的一条道路的宽.小明站在家里点D处观察B,C两点的俯角分别为60°和45°,已知DA垂直地面,则这条道路的宽BC为21.96米($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 据每日邮报报道,按照美国创业家伊隆•马斯克(Elon Musk)最近提出的“超级高铁”(Hyperloop)的设计,超级高铁的速度在理想状态下最高可以达到时速6500公里,预计从北京到纽约仅需2小时,但造价极高,每8公里造价高达620000000美元,数据620000000用科学记数法表示为( )
据每日邮报报道,按照美国创业家伊隆•马斯克(Elon Musk)最近提出的“超级高铁”(Hyperloop)的设计,超级高铁的速度在理想状态下最高可以达到时速6500公里,预计从北京到纽约仅需2小时,但造价极高,每8公里造价高达620000000美元,数据620000000用科学记数法表示为( )| A. | 6.2×109 | B. | 6.2×108 | C. | 62×108 | D. | 0.62×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
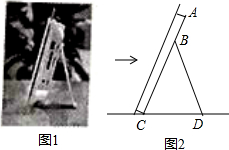 如图1是小红同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=18cm,∠CBD=40°,则点B到CD的距离为16.9cm(用科学计算器计算.参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm).
如图1是小红同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=18cm,∠CBD=40°,则点B到CD的距离为16.9cm(用科学计算器计算.参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com