
”¾ĢāÄæ”æĶõ»Ŗ”¢ÕÅĪ°Į½Ī»Ķ¬Ń§·Ö±š½«×Ō¼ŗ10“ĪŹżŃ§×ŌĪŅ¼ģ²āµÄ³É¼Ø»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼£ŗ
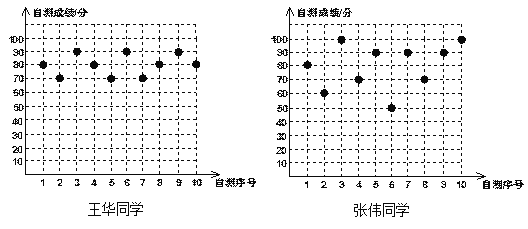
£Ø1£©øł¾ŻÉĻĶ¼ÖŠĢį¹©µÄŹż¾ŻĮŠ³öČēĻĀĶ³¼Ę±ķ£ŗ
Ę½¾ł³É¼Ø£Ø·Ö£© | ÖŠĪ»Źż£Ø·Ö£© | ÖŚŹż£Ø·Ö£© | ·½²ī£ØS2£© | |
Ķõ»Ŗ | 80 | b | 80 | d |
ÕÅĪ° | a | 85 | c | 260 |
Ōņa= £¬b= £¬c= £¬d= £¬
£Ø2£©½«90·ÖŅŌÉĻ£Øŗ¬90·Ö£©µÄ³É¼ØŹÓĪŖÓÅŠć£¬ŌņÓÅŠćĀŹøߵďĒ .
£Ø3£©ĻÖŌŚŅŖ“ÓÕāĮ½øöĶ¬Ń§Ń”Ņ»Ī»Č„²Ī¼ÓŹżŃ§¾ŗČü£¬ÄćæÉŅŌøł¾ŻŅŌÉĻµÄŹż¾ŻøųĄĻŹ¦ÄÄŠ©½ØŅé£æ
”¾“š°ø”æ£Ø1£©80£¬80£¬90£¬60£»£Ø2£©ÕÅĪ°£»£Ø3£©“š°ø¼ū½āĪö
”¾½āĪö”æ£Ø1£©ÓÉĘ½¾łŹż”¢·½²īµÄ¹«Ź½¼ĘĖćĘ½¾ł³É¼Ø¼“æÉ£»½«Ķõ»ŖµÄ³É¼Ø°““óŠ”Ė³ŠņÅÅĮŠ£¬ÖŠ¼äĮ½øöŹżµÄĘ½¾łŹż£¬¼“ĪŖÖŠĪ»Źż£»Ņ»×鏿¾ŻÖŠ³öĻÖ“ĪŹż×ī¶ąµÄŅ»øöŹż¼“ĪŖÖŚŹż£»
£Ø2£©±Č½ĻÄÄĪ»Ķ¬Ń§µÄ³É¼ØŌŚ90·ÖŅŌÉĻ£Øŗ¬90·Ö£©µÄ³É¼Ø¶ą£¬¼“ÓÅŠćĀŹøߣ»
£Ø3£©²»Ķ¬·ÖĪö½Ē¶Č£¬µĆµ½µÄ½į¹ū²»Ķ¬£¬Ö»ŅŖ½ØŅéŗĻĄķ¾ĶŠŠ£¬Čē£ŗ±Č½ĻÕāĮ½Ī»Ķ¬Ń§µÄ·½²ī£¬·½²īŌ½Š”£¬³É¼ØŌ½ĪČ¶Ø£®
½ā£ŗ£Ø1£©”ß![]() ÕÅĪ° =£Ø80+60+100+70+90+50+90+70+90+100£©”Ā10=80£¬
ÕÅĪ° =£Ø80+60+100+70+90+50+90+70+90+100£©”Ā10=80£¬
”ą![]()
”ßS Ķõ»Ŗ 2 =60£¬
”ą![]()
”ßÕÅĪ°µÄ³É¼ØÖŠ90·Ö³öĻֵēĪŹż×ī¶ą£¬ŌņÕÅĪ°µÄ³É¼ØµÄÖŚŹżĪŖ90£»
”ą![]()
¹Ź“š°øĪŖ£ŗ a=80 £¬b=80£¬c=90£¬d=60 £¬
£Ø2£©ÕÅĪ°³É¼ØµÄÓÅŠćĀŹ=50%£¬Ķõ»Ŗ³É¼ØµÄÓÅŠćĀŹ=30%£¬
”ąÓÅŠćĀŹøßµÄĶ¬Ń§ŹĒÕÅĪ°£»
¹Ź“š°øĪŖ£ŗÕÅĪ°.
£Ø3£©”ßS Ķõ»Ŗ2 £¼S ÕÅĪ°2 £¬
”ąŃ”Ķõ»ŖČ„²Ī¼ÓŹżŃ§¾ŗČü.£Øøł¾ŻŅŌÉĻŹż¾ŻĢį¹©µÄ½ØŅéŗĻĄķ¼“æÉ£©



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø12·Ö£©ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬ŅŌABĪŖÖ±¾¶µÄ”ŃO·Ö±š½»BC£¬ACÓŚµćD£¬E£¬DG”ĶACÓŚµćG£¬½»ABµÄŃÓ³¤ĻßÓŚµćF£®
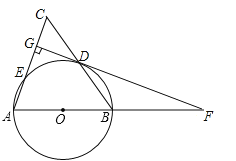
£Ø1£©ĒóÖ¤£ŗÖ±ĻßFGŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©ČōAC=10£¬cosA=![]() £¬ĒóCGµÄ³¤£®
£¬ĒóCGµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
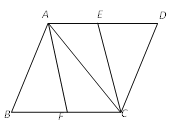
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”õABCDÖŠ£¬E”¢F·Ö±šŹĒAD”¢BCµÄÖŠµć£¬Į¬½ÓAC”¢CE”¢AF£®
£Ø1£©ĒóÖ¤”÷ABF ”Õ ”÷CDE£»
£Ø2£©ČōAB£½AC£¬ĒóÖ¤ĖıߊĪAFCEŹĒ¾ŲŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻA=60”ć£¬BD£¬CD·Ö±šĘ½·Ö”ĻABC£¬”ĻACB£¬M£¬N£¬Q·Ö±šŌŚDB£¬DC£¬BCµÄŃÓ³¤ĻßÉĻ£¬BE£¬CE·Ö±šĘ½·Ö”ĻMBC£¬”ĻBCN£¬BF£¬CF·Ö±šĘ½·Ö”ĻEBC£¬”ĻECQ£¬Ōņ”ĻF= £® 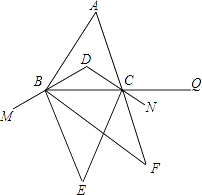
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠŌĖĖćÕżČ·µÄŹĒ£Ø””””£©
A.x5+x5=x10
B.£Øx3£©3=x6
C.x3x2=x5
D.x6©x3=x3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°ŃÅ×ĪļĻßy£½x2ĻČĻņ×óĘ½ŅĘ1øöµ„Ī»³¤¶Č£¬ŌŁĻņĻĀĘ½ŅĘ3øöµ„Ī»³¤¶Č£¬µĆµ½ŠĀµÄÅ×ĪļĻß½āĪöŹ½ĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĆęµÄ²ÄĮĻ:
ČēĶ¼¢Ł£¬ŌŚ![]() ÖŠ£¬ŹŌĖµĆ÷
ÖŠ£¬ŹŌĖµĆ÷![]() .
.
·ÖĪö:Ķعż»Ę½ŠŠĻߣ¬½«![]() ”¢
Ӣ![]() Ӣ
”¢![]() ×÷µČĮæ“ś»»£¬Ź¹ø÷½ĒÖ®ŗĶĒ”ĪŖŅ»øöĘ½½Ē£¬ŅĄøØÖśĻß²»Ķ¬¶ųµĆ¶ąÖÖ·½·Ø.
×÷µČĮæ“ś»»£¬Ź¹ø÷½ĒÖ®ŗĶĒ”ĪŖŅ»øöĘ½½Ē£¬ŅĄøØÖśĻß²»Ķ¬¶ųµĆ¶ąÖÖ·½·Ø.
½ā:ČēĶ¼¢Ś£¬ŃÓ³¤![]() µ½µć
µ½µć![]() ,¹żµć
,¹żµć![]() ×÷
×÷![]() //
//![]() .
.
ŅņĪŖ![]() //
//![]() (×÷Ķ¼ĖłÖŖ)£¬
(×÷Ķ¼ĖłÖŖ)£¬
ĖłŅŌ![]() ,
,![]() (Į½Ö±ĻßĘ½ŠŠ£¬Ķ¬Ī»½Ē”¢ÄŚ“ķ½ĒĻąµČ).
(Į½Ö±ĻßĘ½ŠŠ£¬Ķ¬Ī»½Ē”¢ÄŚ“ķ½ĒĻąµČ).
ÓÖŅņĪŖ![]() (Ę½½ĒµÄ¶ØŅå)£¬
(Ę½½ĒµÄ¶ØŅå)£¬
ĖłŅŌ![]() (µČĮæ“ś»»).
(µČĮæ“ś»»).
ČēĶ¼¢Ū£¬¹ż![]() ÉĻČĪŅ»µć
ÉĻČĪŅ»µć![]() £¬×÷
£¬×÷![]() //
//![]() ,
, ![]() //
//![]() £¬ÕāÖÖĢķ¼ÓøØÖśĻߵķ½·ØÄÜĖµ
£¬ÕāÖÖĢķ¼ÓøØÖśĻߵķ½·ØÄÜĖµ![]() Āš?²¢ĖµĆ÷ĄķÓÉ.
Āš?²¢ĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
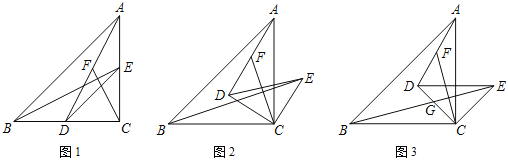
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB£½90”ć£¬AC£½BC£¬D£¬E·Ö±šĪŖAC£¬BCÉĻµÄµć£¬ĒŅCE£½CD£¬Į¬½ÓDE£¬AD£¬BE£¬FĪŖĻ߶ĪADµÄÖŠµć£¬Į¬½ÓCF£®
£Ø1£©ĒóÖ¤£ŗBE£½2CF£»
£Ø2£©ČēĶ¼2£¬°Ń”÷DECČʵćCĖ³Ź±ÕėŠż×Ŗ¦Į½Ē£Ø0”ć£¼¦Į£¼90”ć£©£¬ĘäĖūĢõ¼ž²»±ä£¬ŹŌĢ½¾æĻ߶ĪBEÓėCFµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ČēĶ¼3£¬°Ń”÷DECČʵćCĖ³Ź±ÕėŠż×Ŗ45”ć£¬BE£¬CD½»ÓŚµćG£®Čō”ĻDCF£½30”ć£¬Ēó![]() ¼°
¼°![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com