
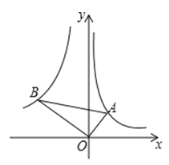
【题目】如图,点![]() ,
,![]() 分别在反比例函数
分别在反比例函数![]()
![]() ,
,![]()
![]() 的图象上.若
的图象上.若![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
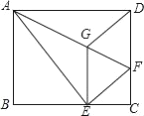
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF×AF;
GF×AF;
(3)若![]() ,折痕AF=5
,折痕AF=5![]() cm,则矩形ABCD的周长为 .
cm,则矩形ABCD的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解决问题:
材料1:对于一个三位数其十位数字等于个位数字与百位数字的差的两倍,则我们称这样的数为“倍差数”如122,![]() ;
;
材料2:若一个数![]() 能够写成
能够写成![]() 均为正整数,且
均为正整数,且![]() ,则我们称这样的数为“不完全平方差数”,
,则我们称这样的数为“不完全平方差数”,![]() 最大时,我们称此时的
最大时,我们称此时的![]() 、
、![]() 为
为![]() 的一组“最优分解数”,井规定
的一组“最优分解数”,井规定![]() .例如
.例如![]() ,因为:
,因为:![]() ,
,![]() ,
,![]() ,所以
,所以![]() ;
;
(1)求证:任意的一个“倍差数”与其百位数字之和能够被3整除;
(2)若一个小于300的三位数![]() 其中
其中![]() ,
,![]() ,且
,且![]() 均为整数)既是一个“不完全平方差数”,也是一个“倍差数”,求所有
均为整数)既是一个“不完全平方差数”,也是一个“倍差数”,求所有![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
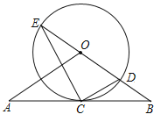
【题目】已知:如图,在△OAB中,OA=OB,⊙O经过AB的中点C,与OB交于点D,且与BO的延长线交于点E,连接EC,CD.
(1)试判断AB与⊙O的位置关系,并加以证明;
(2)若tanE=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
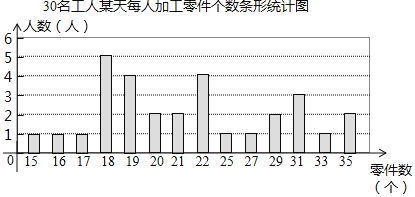
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:
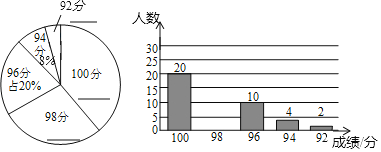
(1)计算样本中,成绩为98分的教师有 人,并补全两个统计图;
(2)样本中,测试成绩的众数是 ,中位数是 ;
(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() .
.
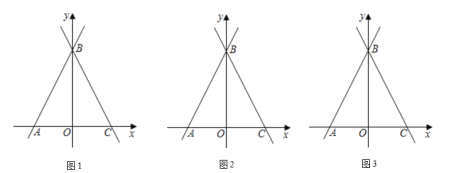
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]()
![]() ,求
,求![]() 与
与![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 时,求直线
时,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
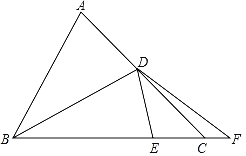
【题目】△ABC中,∠ACB=45°,D为AC上一点,AD=5![]() ,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=
,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=![]() ,则DF长为( )
,则DF长为( )
A.![]() B.
B.![]() C.5
C.5![]() D.7
D.7![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com