
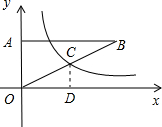
 如图,在平面直角坐标系中,Rt△AOB的直角顶点A在y轴的正半轴上,顶点B在第一象限,函数y=$\frac{k}{x}$的图象与边OB交于点C,且点C为边OB的中点.若△AOB的面积为12,则k的值为6.
如图,在平面直角坐标系中,Rt△AOB的直角顶点A在y轴的正半轴上,顶点B在第一象限,函数y=$\frac{k}{x}$的图象与边OB交于点C,且点C为边OB的中点.若△AOB的面积为12,则k的值为6. 分析 过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,由此可知△ODC∽△OEB,CD∥BE,结合△AOB为直角三角形可得出四边形OEBA为矩形,从而得出“BE=AO,AB=OE”,再由点C为线段OB的中点,即可得出“BE=2CD,OE=2OD”,结合三角形的面积公式以及反比例函数系数k的几何意义即可得出|k|=6,结合反比例函数在第一象限内有图象即可得出结论.
解答 解:过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,如图所示.
∵CD⊥x轴,BE⊥x轴,
∴△ODC∽△OEB,CD∥BE.
∵△AOB为直角三角形,
∴∠OAB=90°=∠AOE,
∴AB∥OE,
∴四边形OEBA为矩形,
∴BE=AO,AB=OE.
又∵点C为线段OB的中点,
∴BE=2CD,OE=2OD.
∵S△AOB=$\frac{1}{2}$AO•AB=$\frac{1}{2}$BE•OE=$\frac{1}{2}$•(2CD)•(2OD)=4S△OCD=12,
∴S△OCD=3=$\frac{1}{2}$|k|,解得:|k|=6.
∵反比例函数图象有一部分在第一象限内,
∴k=6.
故答案为:6.
点评 本题考查了反比例函数与一次函数的交点问题、三角形的面积公式、相似三角形的判定及性质以及反比例函数系数k的几何意义,解题的关键是找出S△AOB=4S△OCD.本题属于基础题,难度不大,解决该题型题目时,根据三角形的面积结合反比例系数k的几何意义找出|k|的值是关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
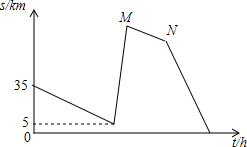 甲、乙两车准备从A地开往B地,由于甲车比乙车慢,所以甲车先出发半小时后乙车再追赶甲车,当乙车出发3h到达一丁字路口时,改变了行进方向,行进了40km后发现选错了行进方向,于是立即调转车头按原速继续追赶甲车,当乙车又追赶了1h后,甲车到达了B地,再行进过程中两车都保持匀速.甲、乙两车间的路程s(单位:km)与乙车行驶的时间t(单位:h)之间的函数图象如图所示,请根据图象信息解答下列问题:
甲、乙两车准备从A地开往B地,由于甲车比乙车慢,所以甲车先出发半小时后乙车再追赶甲车,当乙车出发3h到达一丁字路口时,改变了行进方向,行进了40km后发现选错了行进方向,于是立即调转车头按原速继续追赶甲车,当乙车又追赶了1h后,甲车到达了B地,再行进过程中两车都保持匀速.甲、乙两车间的路程s(单位:km)与乙车行驶的时间t(单位:h)之间的函数图象如图所示,请根据图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5$<\sqrt{5}$ | B. | -$\sqrt{5}$$>-\sqrt{3}$ | C. | $\sqrt{5}-3$$<3-\sqrt{5}$ | D. | 0$<\sqrt{5}-3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在四边形ABCD中,AB⊥BC,AC⊥CD,以CD为直径作半圆O,AB=4cm,BC=3cm,AD=13cm.求图中阴影部分的面积:
如图所示,在四边形ABCD中,AB⊥BC,AC⊥CD,以CD为直径作半圆O,AB=4cm,BC=3cm,AD=13cm.求图中阴影部分的面积:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
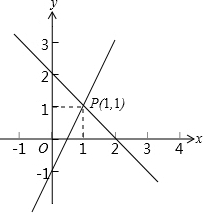 用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象如图所示,则所解的二元一次方程组是( )
用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象如图所示,则所解的二元一次方程组是( )| A. | $\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=1}\\{3x-2y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x-y=1}\\{3x+2y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=2}\\{3x-2y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.
如图,在?ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com