
如图,直线y=x﹣1与反比例函数y= 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
⑴求反比例函数的解析式;
⑵若点P(n,1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
⑶若B(2,1),当x为何值时,一次函数的值大于反比例函数的值
(1)反比例函数解析式为:y=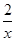 ;
;
(2)S△CEF = .
.
(3)当x>2或- 1<x<0时,一次函数的值大于反比例函数的值.
解析试题分析:(1)将点A的坐标代入直线解析式求出m的值,再将点A的坐标代入反比例函数解析式可求出k的值,继而得出反比例函数关系式;
(2)将点P的纵坐标代入反比例函数解析式可求出点P的横坐标,将点P的横坐标和点F的横坐标相等,将点F的横坐标代入直线解析式可求出点F的纵坐标,将点的坐标转换为线段的长度后,即可计算△CEF的面积;
(3)直接根据图像即可得到.
试题解析:(1)将点A的坐标代入y=x﹣1,可得:m=﹣1﹣1=﹣2,
将点A(﹣1,﹣2)代入反比例函数y= ,可得:k=﹣1×(﹣2)=2,
,可得:k=﹣1×(﹣2)=2,
故反比例函数解析式为:y=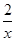 ;
;
(2)将点P的纵坐标y=﹣1,代入反比例函数关系式可得:x=﹣2,
将点F的横坐标x=﹣2代入直线解析式可得:y=﹣3,
故可得EF=3,CE=OE+OC=2+1=3,
故可得S△CEF= CE×EF=
CE×EF= .
.
(3)根据图象可知:当x>2或- 1<x<0时,一次函数的值大于反比例函数的值,
考点:反比例函数与一次函数的交点问题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:填空题
如图,A、B是反比例函数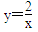 的图象上的两点.AC、BD 都垂直于x轴,垂足分别为C、D,AB的延长线交x轴于点E.若C、D的坐标分别为(1,0)、(4,0),则ΔBDE的面积 与ΔACE的面积的比值是__________.
的图象上的两点.AC、BD 都垂直于x轴,垂足分别为C、D,AB的延长线交x轴于点E.若C、D的坐标分别为(1,0)、(4,0),则ΔBDE的面积 与ΔACE的面积的比值是__________. 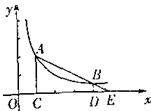
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
六•一儿童节,小文到公园游玩,看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等,比如:A、B、C是弯道MN上任三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等. 爱好数学的他建立了平面直角坐标系(如图).图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米),OG=GH=HI.
(1)求S1和S3的值;
(2)设T 是弯道MN上的任一点,写出y关于x的函数关系式;
是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改选,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知?ABCD水平放置在平面直角坐标系xOy中,若点A,D的坐标分别为(-2,5),(0,1),点B(3,5)在反比例函数y= (x>0)图象上.
(x>0)图象上.
(1)求反比例函数y= 的解析式;
的解析式;
(2)将?ABCD沿x轴正方向平移10个单位后,能否使点C落在反比例函数y= 的图象上?并说明理由.
的图象上?并说明理由.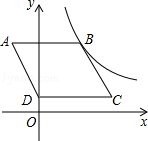
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
如图,已知点A(-4,2)、B( n,-4)是一次函数 的图象与反比例函数
的图象与反比例函数 图象的两个交点
图象的两个交点
【小题1】求此反比例函数的解析式和点B的坐标
【小题2】根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com