
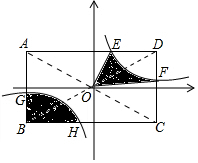
 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与对角线交点在原点的矩形ABCD交于点E,F,G,H且E(1,3),AB:BC=$\frac{1}{2}$,图中阴影部分的面积为15.
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与对角线交点在原点的矩形ABCD交于点E,F,G,H且E(1,3),AB:BC=$\frac{1}{2}$,图中阴影部分的面积为15. 分析 利用反比例函数的对称性可得出阴影部分面积为:$\frac{1}{4}$S矩形ABCD-S△MOE-S△FON,进而得出答案.
解答 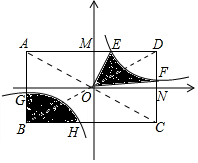 解:由反比例函数的对称性可得,阴影部分面积为:
解:由反比例函数的对称性可得,阴影部分面积为:
$\frac{1}{4}$S矩形ABCD-S△MOE-S△FON
=$\frac{1}{4}$S矩形ABCD-2×$\frac{1}{2}$×1×3,
∵E(1,3),AB:BC=$\frac{1}{2}$,
∴AB=6,BC=12,
则$\frac{1}{4}$S矩形ABCD-2×$\frac{1}{2}$×1×3
=$\frac{1}{4}$×6×12-3
=15.
故答案为:15.
点评 此题主要考查了反比例函数的对称性,正确转化图形面积是解题关键.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:填空题
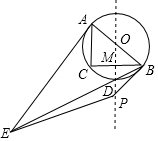 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,圆O是△ABC的外接圆,点M是CB的中点,连接OM并延长交劣弧$\widehat{BC}$于点D,连接BD并延长与过点A的切线交于点E,P是直线OD上一个动点,当|PE-PB|有最大值时,PD的长度是$\frac{165}{74}$.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,圆O是△ABC的外接圆,点M是CB的中点,连接OM并延长交劣弧$\widehat{BC}$于点D,连接BD并延长与过点A的切线交于点E,P是直线OD上一个动点,当|PE-PB|有最大值时,PD的长度是$\frac{165}{74}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
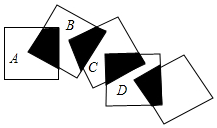 将5个边长都是2cm的正方形如图所示摆放,点A、B、C、D分别是四个正方形对角线的交点,则阴影部分的面积为( )
将5个边长都是2cm的正方形如图所示摆放,点A、B、C、D分别是四个正方形对角线的交点,则阴影部分的面积为( )| A. | 2cm2 | B. | 4cm2 | C. | 6cm2 | D. | 8cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB-BC-CD是一根三节棍,其中线段AB、BC、CD首尾顺次相连,且AB=BC=CD,将这个三节棍摆放在△AMD中,使它的两个端点与△AMD两个顶点重合,三节棍的首尾两节在△AMD的边上,则AB-BC-CD就是△AMD的配套三节棍.
如图,AB-BC-CD是一根三节棍,其中线段AB、BC、CD首尾顺次相连,且AB=BC=CD,将这个三节棍摆放在△AMD中,使它的两个端点与△AMD两个顶点重合,三节棍的首尾两节在△AMD的边上,则AB-BC-CD就是△AMD的配套三节棍.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=x2=3 | B. | x1=x2=1 | C. | x1=x2=-1 | D. | x1=x2=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
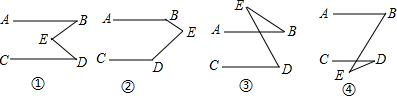
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com