��2013•������һģ��
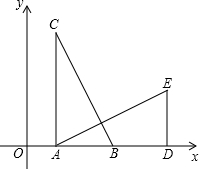
��ͼ��Rt��ADE����Rt��CAB��ת���ɣ���B�Ķ�Ӧ����E����A�Ķ�Ӧ����D����B��C������ֱ�Ϊ��3��0������1��4����
��1��д����E�����꣬�����ó߹���ͼֱ����ͼ��������ת����Q��������ͼ�ۼ�����д��������
��2����ֱ��AE��Ӧ�ĺ�����ϵʽ��
��3������ADE�ش�ֱ��x����߶�PT�۵�������T��x���ϣ���P��AE�ϣ�P��A��E���غϣ���ͼ��ʹ��A����x���ϣ���A�Ķ�Ӧ��Ϊ��F�����T������Ϊ��x��0������PTF���ADE�ص����ֵ����ΪS��
�������S��x֮��ĺ�����ϵʽ�������Ա���x��ȡֵ��Χ����
�ڵ�xΪ��ֵʱ��S�����������ֵ�Ƕ��٣�
���Ƿ���������ĵ�T��ʹ�á�PEFΪֱ�������Σ������ڣ�ֱ��д����T�����ꣻ�������ڣ���˵�����ɣ�

 ��2013•������һģ��
��2013•������һģ�� ��ͼ��Rt��ADE����Rt��CAB��ת���ɣ���B�Ķ�Ӧ����E����A�Ķ�Ӧ����D����B��C������ֱ�Ϊ��3��0������1��4����
��ͼ��Rt��ADE����Rt��CAB��ת���ɣ���B�Ķ�Ӧ����E����A�Ķ�Ӧ����D����B��C������ֱ�Ϊ��3��0������1��4����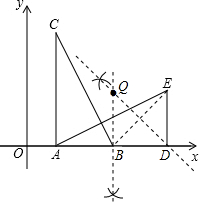 �⣺��1����Rt��ADE����Rt��CAB��ת���ɣ���B�Ķ�Ӧ����E����A�Ķ�Ӧ����D��
�⣺��1����Rt��ADE����Rt��CAB��ת���ɣ���B�Ķ�Ӧ����E����A�Ķ�Ӧ����D�� ��3���ٷ����������
��3���ٷ����������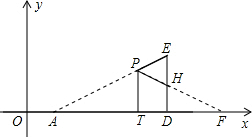 ��ii������F�ڵ�D���ұ�ʱ���ص�����������PTDH��
��ii������F�ڵ�D���ұ�ʱ���ص�����������PTDH��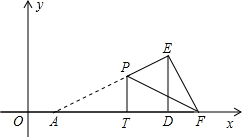 �۴��������ĵ�T��
�۴��������ĵ�T��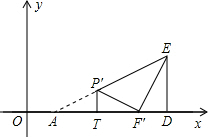 ��ii������P��F��E�Ե�F��Ϊֱ�Ƕ���ʱ����ͼ��
��ii������P��F��E�Ե�F��Ϊֱ�Ƕ���ʱ����ͼ��

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�