
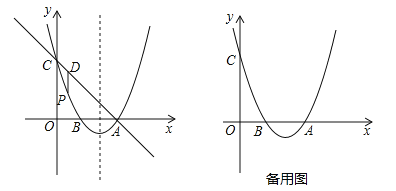
【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.
【答案】(1)y=x2﹣4x+3;(2)![]() ;(3)点P(1,0)或(2,﹣1);(4)M(2,﹣3).
;(3)点P(1,0)或(2,﹣1);(4)M(2,﹣3).
【解析】试题分析:(1)把点A、B的坐标代入抛物线解析式,解方程组得到b、c的值,即可得解;
(2)求出点C的坐标,再利用待定系数法求出直线AC的解析式,再根据抛物线解析式设出点P的坐标,然后表示出PD的长度,再根据二次函数的最值问题解答;
(3)①∠APD是直角时,点P与点B重合,②求出抛物线顶点坐标,然后判断出点P为在抛物线顶点时,∠PAD是直角,分别写出点P的坐标即可;
(4)根据抛物线的对称性可知MA=MB,再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时,|MA﹣MC|最大,然后利用待定系数法求出直线BC的解析式,再求解即可.
试题解析:解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),∴![]() ,解得
,解得![]() ,∴抛物线解析式为y=x2﹣4x+3;
,∴抛物线解析式为y=x2﹣4x+3;
(2)令x=0,则y=3,∴点C(0,3),则直线AC的解析式为y=﹣x+3,设点P(x,x2﹣4x+3).∵PD∥y轴,∴点D(x,﹣x+3),∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣![]() )2+
)2+![]() .∵a=﹣1<0,∴当x=
.∵a=﹣1<0,∴当x=![]() 时,线段PD的长度有最大值
时,线段PD的长度有最大值![]() ;
;
(3)①∠APD是直角时,点P与点B重合,此时,点P(1,0),②∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1).∵A(3,0),∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,此时,点P(2,﹣1).
综上所述:点P(1,0)或(2,﹣1)时,△APD能构成直角三角形;
(4)由抛物线的对称性,对称轴垂直平分AB,∴MA=MB,由三角形的三边关系,|MA﹣MC|<BC,∴当M、B、C三点共线时,|MA﹣MC|最大,为BC的长度,设直线BC的解析式为y=kx+b(k≠0),则![]() ,解得:
,解得: ![]() ,∴直线BC的解析式为y=﹣3x+3.∵抛物线y=x2﹣4x+3的对称轴为直线x=2,∴当x=2时,y=﹣3×2+3=﹣3,∴点M(2,﹣3),即,抛物线对称轴上存在点M(2,﹣3),使|MA﹣MC|最大.
,∴直线BC的解析式为y=﹣3x+3.∵抛物线y=x2﹣4x+3的对称轴为直线x=2,∴当x=2时,y=﹣3×2+3=﹣3,∴点M(2,﹣3),即,抛物线对称轴上存在点M(2,﹣3),使|MA﹣MC|最大.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
【题目】3 月初某商品价格上涨,每件价格上涨 20%.用 3000 元买到的该商品 件数比涨价前少 20 件.3 月下旬该商品开始降价,经过两次降价后,该商品价格为每 件 19.2 元.
(1)求 3 月初该商品上涨后的价格;
(2)若该商品两次降价率相同,求该商品价格的平均降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 在射线
在射线![]() 上(与
上(与![]() 两点不重合),以
两点不重合),以![]() 为边作正方形
为边作正方形![]() ,使点
,使点![]() 与点
与点![]() 在直线
在直线![]() 的异侧,射线
的异侧,射线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
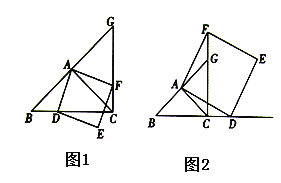
(1)若点![]() 在线段
在线段![]() 上,如图(1),判断:线段
上,如图(1),判断:线段![]() 与线段
与线段![]() 的数量关系: ,位置关系: .
的数量关系: ,位置关系: .
(2)如图(2),①若点![]() 在线段
在线段![]() 的延长线上,(1)中判断线段
的延长线上,(1)中判断线段![]() 与线段
与线段![]() 的数量关系与位置关系是否仍然成立,并说明理由;
的数量关系与位置关系是否仍然成立,并说明理由;
②当![]() 为
为![]() 中点,
中点,![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
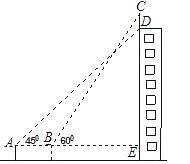
【题目】如图,某幢大楼顶部有一块广告牌CD,甲、乙两人分别在A、B两处,甲测得点D的仰角为45°,乙测得点C的仰角为60°,已知两人使用的测角仪的高度AF、BG相等,且A、B、E三点在一条直线上,AB=8m,BE=15m.求广告牌CD的高(精确到1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开学,两摞规格相同准备发放的数学课本整齐地叠放在讲台上,请根据图中所给的数据信息,解答下列问题:
(1)一本数学课本的高度是多少厘米?
(2)讲台的高度是多少厘米?
(3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示);
(4)若桌面上有56本同样的数学课本,整齐叠放成一摞,从中取走18本后,求余下的数学课本距离地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过 ![]() 元的电器,超出的金额按
元的电器,超出的金额按 ![]() 收取;乙商场规定:凡超过
收取;乙商场规定:凡超过 ![]() 元的电器,超出的金额按
元的电器,超出的金额按 ![]() 收取.某顾客购买的电器价格是
收取.某顾客购买的电器价格是 ![]() 元.
元.
(1)当 ![]() 时,该顾客应选择在 商场购买比较合算;
时,该顾客应选择在 商场购买比较合算;
(2)当 ![]() 时,分别用代数式表示在两家商场购买电器所需付的费用;
时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当 ![]() 时,该顾客应选择哪一家商场购买比较合算?说明理由.
时,该顾客应选择哪一家商场购买比较合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如何快速计算1+2+3+…+n 的值呢?
(1)探究:令s=1+2+3+…+n①,则s=n+n-1+…+2+1②
①+②得2s=(n+1)(n+1)+…+(n+1)=n![]() (n+1)
(n+1)
因此![]() _________________.
_________________.
(2)应用:
①计算:![]() ________;
________;
②如图1,一串连续的整数1,2,3,4,…,自上往下排列,最上面一行有一个数,以下各行均比上一行多一个数字,若共有15行数字,则最底下一行最左边的数是_______;

③如图2,一串连续的整数-25,-24,-23,…,按图1方式排列,共有14行数字,求图2中所有数字的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 第一象限内的图象相交于点
第一象限内的图象相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)观察反比例函数![]() 的图象,当
的图象,当![]() 时,请直接写出
时,请直接写出![]() 的取值范围;
的取值范围;
(3)如图,以![]() 为边作菱形
为边作菱形![]() ,使点
,使点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第一象限,双曲线交
在第一象限,双曲线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com