
【题目】为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图中两幅不完整的统计,请你根据图中提供的信息解答下列问题:


(1)在这次调查中共调查了多少名学生?
(2)求7户外活动时间为0.5小时的人数,并补充频数分布直方图;
(3)求表示户外活动时间为2小时的扇形圆心角的度数;
(4)本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数各是多少?
【答案】解:(1)调查人数=32÷40%=80(人)。
(2)0.5小时的人数是:80×20%=16(人)。
补充频数分布直方图如图所示:
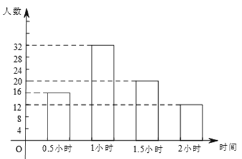
(3)表示户外活动时间2小时的扇形圆心角的度数=![]() ×360°=54°。
×360°=54°。
(4)户外活动的平均时间=![]() =1.175(小时).
=1.175(小时).
∵1.175>1,∴平均活动时间符合上要求。
户外活动时间的众数和中位数均为1。
【解析】(1)根据时间是1小时的有32人,占40%,据此即可求得总人数,
(2)根据总人数乘以百分比即可求得时间是0.5小时的一组的人数,即可作出直方图。
(3)根据360°乘以活动时间是2小时的一组所占的百分比即可求得圆心角的度数。
(3)根据加权平均数公式即可求得平均数,然后与1比较大小即可;根据众数和中位数的定义求出。


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
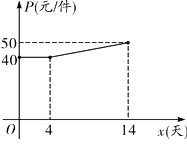
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C在x,y轴正半轴上,反比例函数![]() 过OB的中点D,与BC,AB交于M,N,且已知D(m,2),N(8,n).
过OB的中点D,与BC,AB交于M,N,且已知D(m,2),N(8,n).
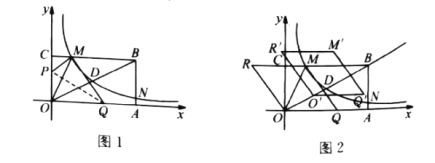
(1)求反比例函数的解析式;
(2)若将矩形一角折叠,使点O与点M重合,折痕为PQ,求点P的坐标;
(3)如图2,若将![]() 沿OM向左翻折,得到菱形OQMR,将该菱形沿射线OB以每秒
沿OM向左翻折,得到菱形OQMR,将该菱形沿射线OB以每秒![]() 个单位向上平移t秒.
个单位向上平移t秒.
① 用t的代数式表示![]() 和
和![]() 的坐标;
的坐标;
② 要使该菱形始终与反比例函数图像有交点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
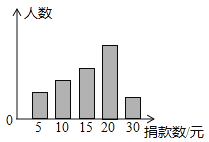
【题目】松雷中学校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
(1)他们一共抽查了多少人?
(2)若该校共有2310名学生,请估计全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
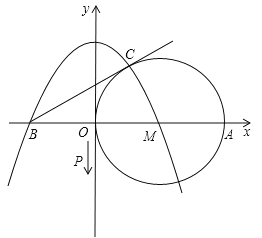
【题目】如图,在平面直角坐标系中,以点M(2,0)为圆心的⊙M与y轴相切于原点O,过点B(﹣2,0)作⊙M的切线,切点为C,抛物线![]() 经过点B和点M.
经过点B和点M.
(1)求这条抛物线解析式;
(2)求点C的坐标,并判断点C是否在(1)中抛物线上;
(3)动点P从原点O出发,沿y轴负半轴以每秒1个单位长的速度向下运动,当运动t秒时到达点Q处.此时△BOQ与△MCB全等,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
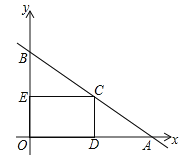
【题目】在平面直角坐标系中,直线AB与x轴、y轴分别交于A(6,0),B(0,3)两点.点C为线段AB上的一个动点,过点C作CD⊥x轴于点D,作CE⊥y轴与点E,求矩形OECD的最大面积,并求此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为
(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为![]() ,直线l的解析式为y=x.
,直线l的解析式为y=x.
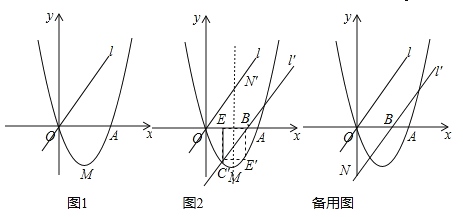
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户种植花生,原来种植的花生亩产量为200千克,出油率为50%(即每100千克花生可加工成花生油50千克).现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量的增长率的二分之一.则新品种花生亩产量的增长率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com