
【题目】如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是 ( )

A. (![]() ,3)、(﹣
,3)、(﹣![]() ,4) B. (
,4) B. (![]() ,3)、(﹣
,3)、(﹣![]() ,4)
,4)
C. (![]() ,
,![]() )、(﹣
)、(﹣![]() ,4) D. (
,4) D. (![]() ,
,![]() )、(﹣
)、(﹣![]() ,4)
,4)
【答案】B
【解析】
首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CG⊥x轴于点G,过点B作BF⊥CG于点F,易得△AOD≌△CBF,△AOD∽△OBE,然后由相似三角形的对应边成比例,求得答案.
如图所示,过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CG⊥x轴于点G,过点B作BF⊥CG于点F,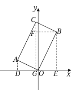
因为四边形AOBC为矩形,所以CB∥AO,CB=AO,因为BF⊥CG,AD⊥x轴,所以∠ADO=∠CFB=90°,因为CB∥AO,DO∥FB,所以∠AOD=∠CBF,在△AOD和△CBF中,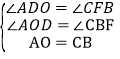 ,所以△AOD≌△CBF(AAS),因为点A的坐标为(-2,1),所以AD=CF=1,DO=FB=2,因为∠BFG=∠FGE=∠BEO=90°,所以四边形BFGE是矩形,所以GE=BF=2,BE=FG,因为点C的纵坐标为4,所以CG=4,BE=FG=CG-CF=4-1=3,因为∠DAO+∠AOD=90°,∠AOB=90°,所以∠AOD+∠BOE=90°,所以∠OAD=∠BOE,同理可得∠AOD=∠OBE,所以△AOD∽△OBE,所以
,所以△AOD≌△CBF(AAS),因为点A的坐标为(-2,1),所以AD=CF=1,DO=FB=2,因为∠BFG=∠FGE=∠BEO=90°,所以四边形BFGE是矩形,所以GE=BF=2,BE=FG,因为点C的纵坐标为4,所以CG=4,BE=FG=CG-CF=4-1=3,因为∠DAO+∠AOD=90°,∠AOB=90°,所以∠AOD+∠BOE=90°,所以∠OAD=∠BOE,同理可得∠AOD=∠OBE,所以△AOD∽△OBE,所以![]() ,即
,即![]() ,解得:OE=
,解得:OE=![]() ,所以GO=GE-OE=2-
,所以GO=GE-OE=2-![]() =
=![]() ,所以点B的坐标为(
,所以点B的坐标为(![]() ,3)点C的坐标为(-
,3)点C的坐标为(-![]() ,4),故答案选B.
,4),故答案选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在面积为60的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=10,BC=12,则CE+CF的值为( )
A. 22-11![]() B.
B. ![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某MP3生产商2014年各季度的产值情况如下表:(单位:万元) 季度第一季度第二季度第三季度第四季度产值10205060.
(1)根据表中的数据绘制成折线统计图;
(2)第四季度的产值比第一季度的产值增加百分之几?
季度 | 第一季度 | 第二季度 | 第三季度 | 第四季度 |
产值 | 10 | 20 | 50 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两点![]() 、
、![]() 在数轴上,
在数轴上,![]() ,点
,点![]() 表示的数是
表示的数是![]() ,且
,且![]() 与
与![]() 互为相反数.
互为相反数.
(1)写出点![]() 表示的数;
表示的数;
(2)如图1,当点![]() 、
、![]() 位于原点
位于原点![]() 的同侧时,动点
的同侧时,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 处在数轴上同时相向而行,动点
处在数轴上同时相向而行,动点![]() 的速度是动点
的速度是动点![]() 的速度的2倍,3秒后两动点相遇,当动点
的速度的2倍,3秒后两动点相遇,当动点![]() 到达点4时,运动停止.在整个运动过程中,当
到达点4时,运动停止.在整个运动过程中,当![]() 时,求点
时,求点![]() 、
、![]() 所表示的数;
所表示的数;
(3)如图2,当点![]() 、
、![]() 位于原点
位于原点![]() 的异侧时,动点
的异侧时,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 处在数轴上向右运动,动点
处在数轴上向右运动,动点![]() 比动点
比动点![]() 晚出发1秒;当动点
晚出发1秒;当动点![]() 运动2秒后,动点
运动2秒后,动点![]() 到达点
到达点![]() 处,此时动点
处,此时动点![]() 立即掉头以原速向左运动3秒恰与动点
立即掉头以原速向左运动3秒恰与动点![]() 相遇;相遇后动点
相遇;相遇后动点![]() 又立即掉头以原速向右运动5秒,此时动点
又立即掉头以原速向右运动5秒,此时动点![]() 到达点
到达点![]() 处,动点
处,动点![]() 到达点
到达点![]() 处,当
处,当![]() 时,求动点
时,求动点![]() 、
、![]() 运动的速度.
运动的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知AB=12cm,点C为线段AB上的一个动点,点D、E分别是AC、BC的中点.

①若点C恰为AB的中点,则DE=______cm.
②若AC=4cm,则DE=_____cm.
③DE的长度与点C的位置是否有关?请说明理由.
(2)如图2,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别是∠AOC、∠BOC的平分线,则∠DOE的大小与射线OC的位置是否有关?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为______(用含t的代数式表示).
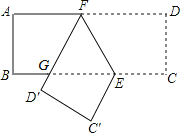
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两张长为4,宽为1的矩形纸条交叉并旋转,使重叠部分成为一个菱形.旋转过程中,当两张纸条垂直时,菱形周长的最小值是4,那么菱形周长的最大值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com