Question

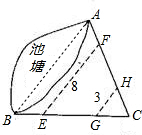
楠楠想出了一个测量池塘的两端A，B的距离的办法：引两条直线AC，BC相交于点C，在BC上取点E，G，使BE=CG，再分别过E，G作EF∥AB，GH∥AB，交AC于F，H．测出EF=8m，GH=3m，她就得出了结论：池塘的宽AB为11m．你认为她说的对吗？

Answer 1

分析：首先根据题意画出图形，可通过两步相似来判断她的做法是否正确，由△CGH∽△CBA，得到CG、HG、CB、AB的比例关系，根据△CEF∽△CBA，得到CE、EF、CB、BA的比例关系，两式相加，利用BE=CG的条件即可判断出所求的结论是否正确．

解答：解：我认为她说的对．理由如下：
解法（1）如图，BE=CG，GH=3m，EF=8m；
根据题意可知：△CHG∽△CAB，△CFE∽△CAB，则有：

CG

CB

=

HG

AB

，

CE

CB

=

EF

AB

，
设BE=CG=x，BC=y，得：

x

y

=

3

AB

，

y-x

y

=

8

AB

，
两式相加，得：

y

y

=

11

AB

，即AB=11m；
所以她的做法是正确的．
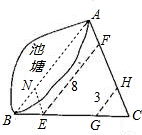
解法（2）：
过E点作EN∥AC交AB于N，如图，
由BE=CG，
∵EN∥AC，
∴∠C=∠BEN，
∵HG∥AB，
∴∠ABE=∠HGC，
在△BEN和△GCH中，
∵

∠ABE=∠HGC BE=GC ∠BEN=∠C

，
∴△BEN≌△GCH（ASA），
∴BN=GH=3，
∵AB∥EF，NE∥AF，
∴四边形ANEF是平行四边形，
∴AN=FE=8，
∴AB=AN+NB=11．

点评：本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．