练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．下列命题是真命题的是（　　）
    A．同位角相等
    B．三角形的三个内角中，至少有一个不大于60°
    C．任何数的零次幂都是1
    D．垂直于同一直线的两条直线互相垂直

    分析 根据平行线的性质、三角形内角和定理、a0=1（a≠0）、在同一平面内，两条直线的位置关系分别进行解答即可得出答案．

    解答 解：A、两直线平行，同位角相等，故本选项错误；
    B、三角形的三个内角中，至少有一个不大于60°，故本选项正确；
    ，故本选项错误；
    C、任何数（零除外）的零次幂都是1，故本选项错误；
    D、在同一平面内，垂直于同一条直线的两条直线互相平行，故本选项错误；
    故选B．

    点评 此题考查了命题与定理，用到的知识点是平行线的性质、三角形内角和定理、a0=1（a≠0）、在同一平面内，两条直线的位置关系；熟练掌握各个定理是本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．若分式$\frac{1}{x-2}$有意义，则x的取值范围为x≠2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

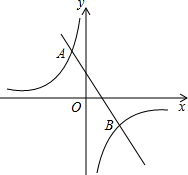    12．如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A（-2，6）和点B（4，n）．
    （1）求着两个函数的解析式
    （2）求直线AB关于y轴的对称直线l的函数解析式
    （3）直线l与反比例函数y=$\frac{m}{x}$的图象是否交点？如果有交点，求出交点的坐标，如果没有交点，可将直线l向上平移多少个单位后，正好与反比例函数的图象有一个交点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图1，在矩形ABCD中，BC＞AB，∠BAD的平分线AF与BD、BC分别交于点E、F，点O是BD的中点，直线OK∥AF，交AD于点K，交BC于点G．
    （1）求证：①△DOK≌△BOG；②AB+AK=BG；
    （2）若KD=KG，BC=4-$\sqrt{2}$．
    ①求KD的长度；
    ②如图2，点P是线段KD上的动点（不与点D、K重合），PM∥DG交KG于点M，PN∥KG交DG于点N，设PD=m，当S△PMN=$\frac{\sqrt{2}}{4}$时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．把多项式9a3-ab2分解因式的结果是a（3a+b）（3a-b）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=-x+4．

    问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线$y=\frac{1}{4}{（{x-m}）^2}+n$经过B、C两点，顶点D在正方形内部．
    （1）直接写出点D（m，n）所有的特征线；
    （2）若点D有一条特征线是y=x+1，求此抛物线的解析式；
    （3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

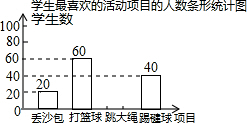    13．我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：
     学生最喜欢的活动项目的人数统计表     
    项目学生数（名）百分比
    丢沙包2010%
    打篮球60p%
    跳大绳n40%
    踢毽球4020%
    根据图表中提供的信息，解答下列问题：
    （1）m=200，n=80，p=30；
    （2）请根据以上信息直接补全条形统计图；
    （3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

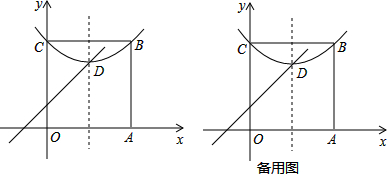
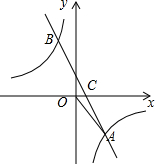    10．如图，已知点A（3，m），B（-2，6）在反比例函数$y=\frac{k}{x}$的图象上，直线AB与x轴交于点C．
    （1）求直线AB的解析式；
    （2）若点D在x轴上，且DC=OA，则求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．某商店在销售西服时，按每套进价的150%标价，后来为吸引消费者，按标价的八折销售，此时每套西服仍可获利120元，求西服的进价为多少元？
    （1）建立一元一次方程模型并解答上述问题；
    （2）解答后请思考以下问题：
    ①在建立一元一次方程的模型解决问题过程中，你认为最关键的是什么？
    ②解一元一次方程的算法，步骤有哪些？
    ③用算术法解决实际问题与建立方程模型解决实际问题，这两种方法有什么不同？你说说哪种方法更优越？

    查看答案和解析>>

    同步练习册答案