Question

探究学习：探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法．请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC，BD为腰AC上的高（如图1）．
（1）若等腰△ABC的面积为24 cm²，腰的长为8 cm，则腰AC上的高BD的长为______cm；
（2）若BD=h，M是直线BC上的任意一点，M到AB、AC的距离分别为h₁、h₂．
①若M在线段BC上，请你结合图2证明：h₁+h₂=h；
②当点M在BC延长线上时，h₁、h₂、h之间的关系为______．（直接写出结论，不必证明）

Answer 1

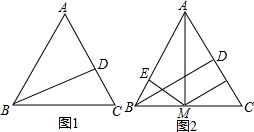
解：（1）∵S_△ABC=AC•BD=×8×BD=24，
∴BD=24÷8×2=6；

（2）
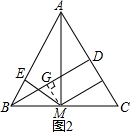
①过M作MG⊥BD，交BD与点G，则MF=DG，MG∥CD，
∴∠GMB=∠C，
∵AB=AC，
∴∠ABC=∠C，
∴∠GMB=∠ABC，
又∵∠MGB=∠BEM=90°，BM=MB，
∴△BME≌△MBG（AAS），
∴BG=ME．
即BD=BG+DG=ME+MF，
∴h₁+h₂=h；

②|h₁-h₂|=h．
分析：（1）利用三角形的面积公式可得，腰AC上的高BD=面积÷AC×2；
（2）过M作MG⊥BD，交BD与点G，则可证MF=DG；再证△BME≌△MBG，得BG=ME．即BD=BG+DG=ME+MF；
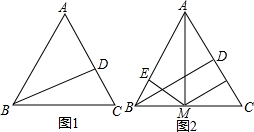
（3）可采用和（2）类似的方法，画图作辅助线，经过证明三角形全等，得出h₁-h₂=h．
点评：此题综合性较强，考查了三角形的面积、全等三角形的判定等知识点，要熟练掌握并灵活应用这些知识．