
【题目】如图,直线![]() 是一次函数
是一次函数![]() 的图象,直线
的图象,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() ,直线
,直线![]() 交于点
交于点![]() ,
,
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(1)求直线![]() 的表达式;
的表达式;
(3)求![]() 的面积.
的面积.
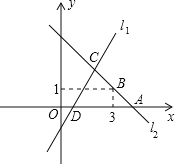
【答案】(1)点D的坐标为(1,0),点C的坐标为(2,2);(2)直线l2的解析式为y=-x+4;(3)S△ADC=3.
【解析】
(1)利用直线l1的解析式令y=0,求出x的值即可得到点D的坐标;把点C的坐标代入直线l1的解析式求出m的值,即可得解;
(2)根据点B、C的坐标,利用待定系数法求一次函数解析式解答;
(3)先求出点A的坐标,再求出AD的长,然后利用三角形的面积公式列式进行计算即可得解;
解:(1)∵点D是直线l1:y=2x-2与x轴的交点,
∴y=0,0=2x-2,x=1,
∴D(1,0),
∵点C在直线l1:y=2x-2上,
∴2=2m-2,m=2,
∴点C的坐标为(2,2);
(2)∵点C(2,2)、B(3,1)在直线l2上,将点代入y=2x-2
∴![]() ,解得:
,解得:![]() ,
,
∴直线l2的解析式为y=-x+4;
(3)∵点A是直线l2与x轴的交点,
∴y=0,
即0=-x+4,
解得x=4,
即点A(4,0),
所以,AD=OA-OD=4-1=3,
因为,点C(2,2)
所以,点C的纵坐标=2
所以,S△ADC=![]() AD·点C的纵坐标=
AD·点C的纵坐标=![]() ×3×2=3;
×3×2=3;


科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AD=4,AB=2![]() ,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
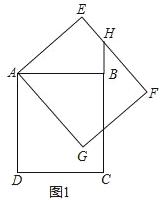
(1)求证:BH=EH;
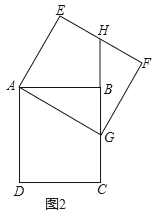
(2)如图2,当点G落在线段BC上时,求点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
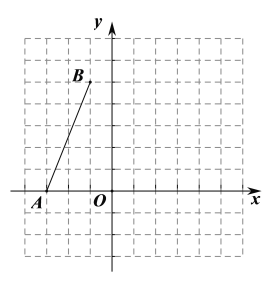
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() .
.
(1)①画出线段![]() 关于
关于![]() 轴对称的线段
轴对称的线段![]() ;
;
②在![]() 轴上找一点
轴上找一点![]() 使
使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(2)按下列步骤,用不带刻度的直尺在线段![]() 找一点
找一点![]() 使
使![]() .
.
①在图中取点![]() ,使得
,使得![]() ,且
,且![]() ,则点
,则点![]() 的坐标为___________;
的坐标为___________;
②连接![]() 交
交![]() 于点
于点![]() ,则点
,则点![]() 即为所求.
即为所求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小岩打算购买气球装扮学校“毕业典礼”活动会场气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位.已知第一束,第二束气球的价格如图所示,则第三束气球的价格为( )
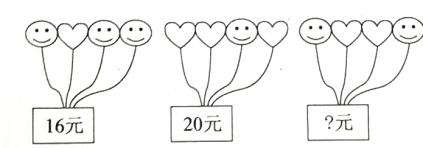
A.15元B.16元C.17元D.18元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知抛物线经过点A(l, 0),B(一3,0),C(0,3)三点.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上,是否存在点M,使得![]() ?若存在求出M点的坐标;若不存在,请说明理由;
?若存在求出M点的坐标;若不存在,请说明理由;
(3)点P是位于直线BC上方的抛物线上的一个动点,是否存在点P,使![]() 的面积最大?若存在,求出P的坐标及
的面积最大?若存在,求出P的坐标及![]() 的最大值:若不存在,说明理由.
的最大值:若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程
解:设x2﹣4x=y,
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的 (填序号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后? .(填“是”或“否”)如果否,直接写出最后的结果 .
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=![]() x+b与x轴交于点A,与y轴交于点B,点P坐标为(3,0),过点P作PC⊥x轴于P,且△ABC为等腰直角三角形.
x+b与x轴交于点A,与y轴交于点B,点P坐标为(3,0),过点P作PC⊥x轴于P,且△ABC为等腰直角三角形.
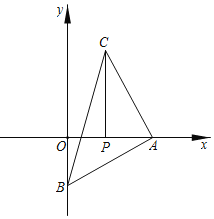
(1)如图,当∠BAC=90°,AB=AC时,求证△ABO≌△CAP;
(2)当AB为直角边时,请直接写出所有可能的b值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过点P(2,﹣3).
(1)求该函数的解析式;
(2)若将点P沿x轴负方向平移3个单位,再沿y轴方向平移n(n>0)个单位得到点P′,使点P′恰好在该函数的图象上,求n的值和点P沿y轴平移的方向.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com