
分析 (1)利用连续整数乘积的倒数等于两整数倒数的差,将原式拆解开,再计算即可得;
(2)先计算括号内的减法,再计算乘法即可得.
解答 解:(1)原式=$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{99}$-$\frac{1}{100}$
=$\frac{1}{2}$-$\frac{1}{100}$
=$\frac{50}{100}$-$\frac{1}{100}$
=$\frac{49}{100}$;
(2)原式=$\frac{99}{100}$×$\frac{98}{99}$×…×$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{100}$.
点评 本题主要考查数字的变化规律,根据题意得出连续整数乘积的倒数等于两整数倒数的差是解题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
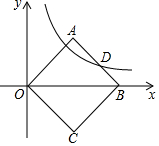 如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.
如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
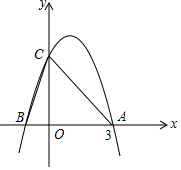 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
在直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com