
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
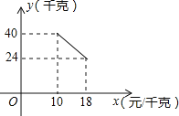
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
【答案】(1)y=﹣2x+60(10≤x≤18);(2)当销售价为18元时,每天的销售利润最大,最大利润是192元;(3)15元.
【解析】
试题分析:首先设y与x的函数关系熟为y=kx+b,然后将(10,40)和(18,24)代入解析式求出k和b的值;根据利润=单件利润×数量得出函数解析式,根据函数的增减性得出最大利润;根据题意列出方程,从而求出x的值.
试题解析:(1)设y与x之间的函数关系式y=kx+b,把(10,40),(18,24)代入得
![]() ,解得
,解得![]() , ∴y与x之间的函数关系式y=﹣2x+60(10≤x≤18);
, ∴y与x之间的函数关系式y=﹣2x+60(10≤x≤18);
(2)W=(x﹣10)(﹣2x+60)=﹣2x2+80x﹣600,
对称轴x=20,在对称轴的左侧y随着x的增大而增大, ∵10≤x≤18,
∴当x=18时,W最大,最大为192. 即当销售价为18元时,每天的销售利润最大,最大利润是192元.
(3)由150=﹣2x2+80x﹣600,
解得x1=15,x2=25(不合题意,舍去)
答:该经销商想要每天获得150元的销售利润,销售价应定为15元.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】已知:OB、OC、OE是∠AOD内的射线,若∠AOD=130°.
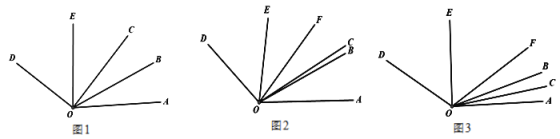
(1)如图1,OB是∠AOC的平分线,OE是∠COD的平分线,∠BOE=_____度;
(2)OF也是∠AOD内的射线,如图2,若∠FOC=20°,OB平分∠AOF,OE平分∠COD,当射线OC绕点O在∠AOF内旋转时,求∠BOE的大小;
(3)在(2)的条件下,当射线OC从边OA开始绕O点以每秒2°的速度逆时针旋转t秒,如图3,若∠AOB:∠DOE=2:3,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
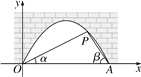
【题目】图中是抛物线型拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α,β,tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少(![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
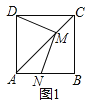
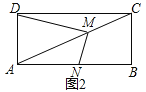
【题目】如图1,点M放在正方形ABCD的对角线AC(不与点A重合)上滑动,连结DM,做MN⊥DM,交直线AB于N.
(1)求证:DM=MN;
(2)若将(1)中的正方形变为矩形,其余条件不变如图,且DC=2AD,求MD:MN的值;
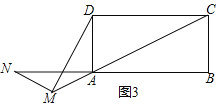
(3)在(2)中,若CD=nAD,当M滑动到CA的延长线上时(如图3),请你直接写出MD:MN的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元.
(1)如果小张家一个月用电128度,那么这个月应缴纳电费多少元?
(2)如果小张家一个月用电a度![]() ,那么这个月应缴纳电费多少元?(用含a的代数式表示)
,那么这个月应缴纳电费多少元?(用含a的代数式表示)
(3)如果这个月缴纳电费为147.8元,那么小张家这个月用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知圆锥底面半径r=10cm,母线长为40cm.

(1)求它的侧面展开图的圆心角和表面积.
(2)若一只甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com