
分析 (1)设售价应为x元,根据不等关系:在7月份销售量不低于1100件,列出不等式求解即可;
(2)先求出8月份的进价,再根据等量关系:8月份利润达到3388元,列出方程求解即可.
解答 解:(1)设售价应为x元,依题意有
1160-$\frac{2(x-12)}{0.1}$≥1100,
解得:x≤15.
答:售价应不高于15元.
(2)10月份的进价:10(1+20%)=12(元),
由题意得:
1100(1+m%)[15(1-$\frac{2}{15}$m%)-12]=3388,
设m%=t,化简得50t2-25t+2=0,
解得:t1=$\frac{2}{5}$,t2=$\frac{1}{10}$,
所以m1=40,m2=10,
因为m>10,
所以m=40.
答:m的值为40.
点评 此题考查了一元一次不等式的应用,一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的不等关系和等量关系,列出不等式和方程,再求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
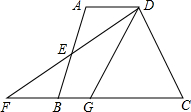 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
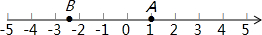 根据下面给出的数轴,解答下面的问题:
根据下面给出的数轴,解答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C是反比例函数y=$\frac{k}{x}$图象的一点,点C的坐标为(4,-1).
如图,点C是反比例函数y=$\frac{k}{x}$图象的一点,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
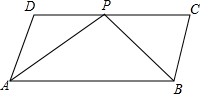 如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com