
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
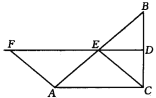
(1)求证:四边形ACEF是平行四边形;
(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
【答案】(1)、证明过程见解析;(2)、∠B=30°,证明过程见解析;(3)、不可能,理由见解析.
【解析】
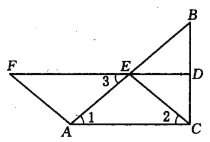
试题分析:(1)、根据DF为垂直平分线得出BD=CD,DF⊥BC,根据∠ACB=∠BDF=90°得出DF∥AC,则BE=AE,则AE=CE,∴∠1=∠2,得到△ACE≌△EFA,即AC=EF,从而得到平行四边形;(2)、当∠B=30°时,AC=![]() AB,CE=
AB,CE=![]() AB,从而得到AC=CE,得到菱形;(3)、根据CE在△ABC内部,∠ACE<∠ACB=90°,则不可能为正方形.
AB,从而得到AC=CE,得到菱形;(3)、根据CE在△ABC内部,∠ACE<∠ACB=90°,则不可能为正方形.
试题解析:(1)、∵DF是BC的垂直平分线 ∴DF⊥BC,DB=DC
∴∠ACB=∠BDF=90° ∴DF∥AC ∴BE=AE
∴AE=CE=![]() AB
AB
∴∠1=∠2
∵EF∥BC,AF=CE=AE
∴∠1=∠2=∠3=∠F
∴△ACE≌△EFA ∴AC=EF
∴四边形ACEF是平行四边形;
(2)、当∠B=30°时,四边形ACEF是菱形.证明如下:
在△ABC中,∠ACB=90°,∠B=30°
∴AC=![]() AB ∵CE=
AB ∵CE=![]() AB ∴AC=CE
AB ∴AC=CE
∴四边形ACEF是菱形
(3)、四边形ACEF不可能是正方形,理由如下:由(1)知E是AB的中点
∴CE在△ABC内部,∴∠ACE<∠ACB=90° ∴四边形ACEF不可能是正方形


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.
(1)求证:EF∥AC;(2)求∠BEF大小;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.

(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
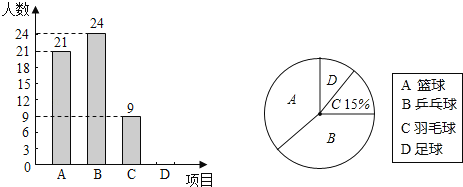
【题目】某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:
(1)这次被抽查的学生有 人;请补全条形统计图;
(2)在统计图2中,“乒乓球”对应扇形的圆心角是 度;
(3)若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要得到y=(x-3)2-2的图象,只要将y=x2的图象( )
A.由向左平移3个单位,再向上平移2个单位;
B.由向右平移3个单位,再向下平移2个单位;
C.由向右平移3个单位,再向上平移2个单位;
D.由向左平移3个单位,再向下平移2个单位.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com