
分析 (1)去掉括号后,再根据有理数的加减运算,即可得出结论;
(2)化小数为分数以及化除为乘,再根据有理数的乘法运算,即可得出结论;
(3)利用乘法分配律将原算式分开,再根据有理数的乘法运算求出每项的值,加减后即可得出结论;
(4)化带分数为假分数,再根据有理数的乘法运算,即可得出结论;
(5)先求出乘方的值以及化除为乘,再根据有理数的乘法运算求出每项的值,相减后即可得出结论.
解答 解:(1)-20+(-14)-(-14)-13=-20-14+14-13=-33;
(2)-1.25×$\frac{1}{8}$÷(-$\frac{2}{5}$)×(-8)=-$\frac{9}{8}$×$\frac{1}{8}$×(-$\frac{5}{2}$)×(-8)=-$\frac{45}{16}$;
(3)($\frac{1}{2}$-$\frac{5}{9}$+$\frac{7}{12}$)×(-36)=$\frac{1}{2}$×(-36)-$\frac{5}{9}$×(-36)+$\frac{7}{12}$×(-36)=-9;
(4)9$\frac{18}{19}$×(-5)=$\frac{189}{19}$×(-5)=-$\frac{945}{19}$;
(5)2×(-3)2-5÷(-$\frac{1}{2}$)×(-2)=2×9-5×(-2)×(-2)=18-20=-2.
点评 本题考查了有理数的混合运算,牢记有理数混合运算的法则及运算顺序是解题的关键.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 24 | C. | 32 | D. | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
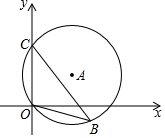 如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=30°,则点C的坐标为 ( )
如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=30°,则点C的坐标为 ( )| A. | (0,5) | B. | (0,5$\sqrt{3}$) | C. | (0,$\frac{5}{2}$$\sqrt{3}$) | D. | (0,$\frac{5}{3}$$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
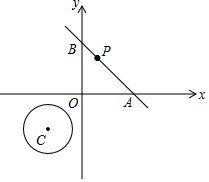 如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为$\sqrt{2}$.函数y=-x+2图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点(包括端点).
如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为$\sqrt{2}$.函数y=-x+2图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点(包括端点).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com