
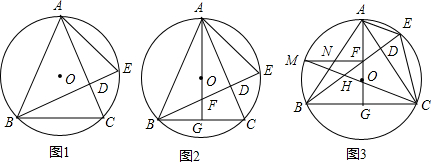
分析 (1)先依据等腰三角形的性质和三角形的内角和定理证明∠BAC+2∠C=180°,然后依据直角三角形两锐角互余以及等式的性质客的到2∠CAE+2∠E=180°,然后根据同弧所对的圆周角相等得到∠E=∠C,最后依据等量代换可得到要证明的结论;
(2)连接OB、OC.先依据SSS证明△ABO≌△ACO,从而得到∠BAO=∠CAO,然后在依据ASA证明△ABF≌△ACE,最后根据全等三角形的性质可证明BF=CE;
(3)连接HG、BM.先依据等腰三角形三线合一的性质证明BG=CG,从而得到HG是△BCD的中位线,接下来证明∠FHO=∠AFD=∠HFO,于是可得到HO=OF,然后依据同角的余角相等客证明∠OGH=∠OHG,从而得到OH=OG,故此可值OF=OG,接下来证明四边形MFGB是矩形,然后由MF∥BC客证明△MFH∽△CBH,从而可证明HF=FD.接下来再证明△ADF≌△GHF,由全等三角形的性质的到AF=FG,然后再证明△MNB≌△NAF,于是得到MN=NF.设S△OHF=S△OHG=a,则S△FHG=2a,S△BHG=4a,然后由S四边形BHOG=5$\sqrt{2}$,可求得a=$\sqrt{2}$,设HF=x,则BH=2x,然后证明△GFH∽△BFG,由相似三角形的性质可得到HG=$\sqrt{2}$x,然后依据S△BHG=$\frac{1}{2}$BH•HG=4$\sqrt{2}$,可求得x=2,故此可得到HB、GH的长,然后依据勾股定理可求得BG的长,于是容易求得MN的长.
解答 解:(1)∵AB=AC,
∴∠ABC=∠ACB.
∴∠BAC+2∠C=180°.
∵BD⊥AC,
∴∠ADE=90°.
∴∠E+∠CAE=90°.
∴2∠CAE+2∠E=180°.
∵∠E=∠C,
∴2∠CAE+2∠C=180°.
∴∠BAC=2∠CAE.
(2)连接OB、OC.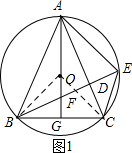
∵AB=AC,AO=AO,OB=OC,
∴△ABO≌△ACO.
∴∠BAO=∠CAO.
∵∠BAC=2∠CAE,
∴∠BAO=∠CAE.
在△ABF和△ACE中,$\left\{\begin{array}{l}{∠ABF=∠ACE}\\{AB=AC}\\{∠BAF=∠CAE}\end{array}\right.$,
∴△ABF≌△ACE.
∴BF=CE.
(3)连接HG、BM.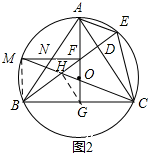
∵AB=AC,∠BAO=∠CAO,
∴AG⊥BC,BG=CG.
∵BH=DH,
∴HG是△BCD的中位线.
∴HG∥CD.
∴∠GHF=∠CDE=90°.
∵OA=OC,
∴∠OAC=∠OCA.
∵∠OAC+∠AFD=90°,∠OCA+∠FHO=90°,
∴∠FHO=∠AFD=∠HFO.
∴HO=OF.
∵∠HFO+∠OGH=90°,∠OHF+∠OHG=90°,
∴∠OGH=∠OHG.
∴OH=OG.
∴OF=OG.
∵OM=OC,
∴四边形MFCG是平行四边形.
又∵MC是圆O的直径,
∴∠CBM=90°.
∴四边形MFGB是矩形.
∴MB=FG,∠FMB=∠AFN=90°.
∵MF∥BC,
∴△MFH∽△CBH.
∴$\frac{HF}{BH}=\frac{MF}{CB}=\frac{1}{2}$.
∴HF:HD=1:2.
∴HF=FD.
在△ADF和△GHF中,$\left\{\begin{array}{l}{∠AFD=∠GFH}\\{∠ADF=∠GHF}\\{FH=FD}\end{array}\right.$,
∴△ADF≌△GHF.
∴AF=FG.
∴MB=AF.
在△MNB和△NAF中,$\left\{\begin{array}{l}{∠BMF=∠AFN=90°}\\{∠ANF=∠BNM}\\{MB=AF}\end{array}\right.$,
∴△MNB≌△NAF.
∴MN=NF.
设S△OHF=S△OHG=a,则S△FHG=2a,S△BHG=4a,
∴S四边形BHOG=5a=5$\sqrt{2}$.
∴a=$\sqrt{2}$.
设HF=x,则BH=2x.
∵∠HHG=∠GFB,∠GHF=∠FGB,
∴△GFH∽△BFG.
∴$\frac{HF}{HG}=\frac{GH}{BH}$,即$\frac{x}{HG}=\frac{HG}{2x}$.
∴HG=$\sqrt{2}$x.
∴S△BHG=$\frac{1}{2}$BH•HG=$\frac{1}{2}$×2x•$\sqrt{2}$x=4$\sqrt{2}$,解得:x=2.
∴HB=4,GH=2$\sqrt{2}$.
由勾股定理可知:BG=2$\sqrt{6}$.
∴MF=2$\sqrt{6}$.
∴MN=NF=$\sqrt{6}$.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了圆周角定理、全等三角形的性质和判定、相似三角形的性质和判断、勾股定理的应用、矩形的性质和判定,找出图中相似三角形和全等三角形是解题的关键.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
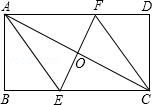 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
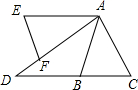 如图,将△ABC纸片绕点A按逆时针方向旋转某个角后得到△AEF,CB、AF的延长线交于点D,AE∥CB,∠D=40°,则∠BAC的度数为( )
如图,将△ABC纸片绕点A按逆时针方向旋转某个角后得到△AEF,CB、AF的延长线交于点D,AE∥CB,∠D=40°,则∠BAC的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
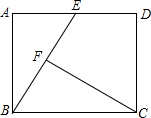 如图,在矩形ABCD中,E是AD边的中点,CF⊥BE,垂足为点F,若BF=EF,AE=1,则AB边的长为( )
如图,在矩形ABCD中,E是AD边的中点,CF⊥BE,垂足为点F,若BF=EF,AE=1,则AB边的长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
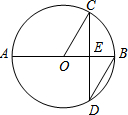 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )| A. | $\frac{5}{2}$cm | B. | 3cm | C. | 3$\sqrt{3}$cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8cm | B. | 5$\sqrt{2}$cm | C. | 5.5cm | D. | 1cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com