
(12分如图,直线l1与x轴、y轴分别交于A、B两点,直线l2与直线l1关于x轴对称,已知直线l1的解析式为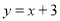 .
.
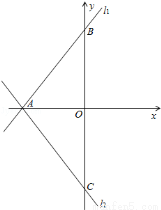
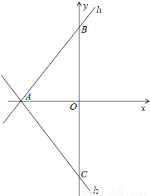
(1)求直线l2的解析式;
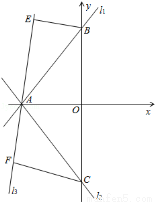
(2)过A点在△ABC的外部作一条直线l3,过点B作BE⊥l3于E,过点C作CF⊥l3于F,请画出图形并求证:BE+CF=EF;
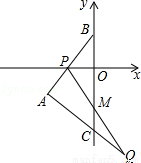
(3)△ABC沿y轴向下平移,AB边交x轴于点P,过P点的直线与AC边的延长线相交于点Q,与y轴相交于点M,且BP=CQ,在△ABC平移的过程中,①OM为定值;②MC为定值.在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值.
(1)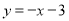 ;(2)作图和证明见试题解析;(3)①对,OM=3.
;(2)作图和证明见试题解析;(3)①对,OM=3.
【解析】
试题分析:(1)根据题意先求直线l1与x轴、y轴的交点A、B的坐标,再根据轴对称的性质求直线l2的上点C的坐标,用待定系数法求直线l2的解析式;
(2)根据题意结合轴对称的性质,先证明△BEA≌△AFC,再根据全等三角形的性质,结合图形证明BE+CF=EF;
(3)首先过Q点作QH⊥y轴于H,证明△QCH≌△PBO,然后根据全等三角形的性质和△QHM≌△POM,从而得HM=OM,根据线段的和差进行计算OM的值.
试题解析:(1)∵直线l1与x轴、y轴分别交于A、B两点,∴A(﹣3,0),B(0,3),∵直线l2与直线l1关于x轴对称,∴C(0,﹣3)∴直线l2的解析式为: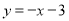 ;
;
(2)如图.BE+CF=EF.∵直线l2与直线l1关于x轴对称,∴AB=AC,∵l1与l2为象限平分线的平行线,∴△OAC与△OAB为等腰直角三角形,∴∠EBA=∠FAC,∵BE⊥l3,CF⊥l3,∴∠BEA=∠AFC=90°,∴△BEA≌△AFC,∴BE=AF,EA=FC,∴BE+CF=AF+EA=EF;
(3)①对,OM=3,过Q点作QH⊥y轴于H,直线l2与直线l1关于x轴对称,∵∠POB=∠QHC=90°,BP=CQ,又∵AB=AC,∴∠ABO=∠ACB=∠HCQ,则△QCH≌△PBO(AAS),∴QH=PO=OB=CH,∴△QHM≌△POM,∴HM=OM,∴OM=BC﹣(OB+CM)=BC﹣(CH+CM)=BC﹣OM,∴OM=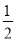 BC=3.
BC=3.

考点:1.轴对称的性质;2.全等三角形的判定与性质.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:2014-2015学年山东东平县梯门中学七年级上学期第三次月考数学试卷(解析版) 题型:选择题
数轴上点A到原点的距离为6,则点A表示的数是( )
A.6和-6 B.6 C.-6 D.3和-3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古巴彦淖尔前旗四中七年级上学期期末考试数学卷(解析版) 题型:填空题
已知单项式3am+2b4与-a5bn-1可以合并同类项,则m+n = ;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古巴彦淖尔前旗四中七年级上学期期末考试数学卷(解析版) 题型:选择题
若x=2是关于x的方程ax+3=5的解,则a的值为( )
A.1 B.-1 C.2 D.-2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏兴化乐吾实验学校等八年级上第三次月考数学试卷(解析版) 题型:解答题
(12分)甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍,乒乓球每盒定价5元,乒乓球拍每副定价20元.现两家商店都搞促销活动,甲店每买一副球拍赠一盒乒乓球;乙店按九折优惠.某班级需购球拍4副,乒乓球x盒(x≥4).
(1)若在甲店购买付款 (元),在乙店购买付款
(元),在乙店购买付款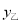 (元),分别写出与x的函数关系式;
(元),分别写出与x的函数关系式;
(2)买30盒乒乓球时,在哪家商店购买合算?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏兴化乐吾实验学校等八年级上第三次月考数学试卷(解析版) 题型:填空题
已知正比例函数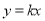 (
(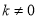 )的图象经过点(-3,-2),则此正比例函数的关系式为_______
)的图象经过点(-3,-2),则此正比例函数的关系式为_______
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市八年级下学期开学考试数学试卷(解析版) 题型:选择题
如图,△ABC中,AB=20㎝,AC=12㎝,点P从点B出发以3㎝/s的速度向点A运动,点Q从点A同时出发以2㎝/s的速度想点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
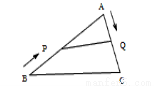
A.2.5s; B.3s; C.3.5s; D.4s
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com