
【题目】教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)将最后一名老师送到目的地时,小王距出发地多少千米?
(2)若汽车耗油量为0.5升/千米,则当天耗油多少升?若汽油价格为6.70元/升,则小王共花费了多少元钱?
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.

(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网上书城“五一·劳动节”期间在特定的书目中举办特价促销活动,有A、B、C、D四本书是小明比较中意的,但是他只打算选购两本,求下列事件的概率:
(1)小明购买A书,再从其余三本书中随机选一款,恰好选中C的概率是_________;
(2)小明随机选取两本书,请用树状图或列表法求出他恰好选中A、C两本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(学习心得)
小刚同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 外一点,且
外一点,且![]() ,求
,求![]() 的度数,若以点
的度数,若以点![]() 为圆心,
为圆心,![]() 为半径作辅助圆⊙
为半径作辅助圆⊙![]() ,则点
,则点![]() 、
、![]() 必在⊙
必在⊙![]() 上,
上,![]() 是⊙
是⊙![]() 的圆心角,而
的圆心角,而![]() 是圆周角,从而可容易得到
是圆周角,从而可容易得到![]() __________
__________![]() .
.
(2)(问题解决)
如图![]() ,在四边形
,在四边形![]() 中,
中,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
小刚同学认为用添加辅助圆的方法,可以使问题快速解决,他是这样思考的:![]() 的外接圆就是以
的外接圆就是以![]() 的中点为圆心,
的中点为圆心,![]() 长为半径的圆;
长为半径的圆;![]() 的外接圆也是以
的外接圆也是以![]() 的中点为圆心,
的中点为圆心,![]() 长为半径的圆.这样
长为半径的圆.这样![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一个圆上,进而可以利用圆周角的性质求出
四点在同一个圆上,进而可以利用圆周角的性质求出![]() 的度数,请运用小刚的思路解决这个问题.
的度数,请运用小刚的思路解决这个问题.
(3)(问题拓展)
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高,且
边上的高,且![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.下面是小文的探究过程,请补充完整:
的图象与性质.下面是小文的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:

如图,在平面直角坐标系![]() 中,描出了以上表中各对应值为坐标的点.
中,描出了以上表中各对应值为坐标的点.
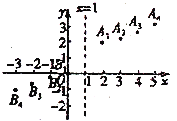
①观察图中各点的位置发现:点![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 均关于某点中心对称,则该点的坐标为__________;
均关于某点中心对称,则该点的坐标为__________;
②小文分析函数![]() 表达式发现:当
表达式发现:当![]() 时,该函数的最大值为0,则该函数图象在直线
时,该函数的最大值为0,则该函数图象在直线![]() 左侧的最高点的坐标为__________;
左侧的最高点的坐标为__________;
(3)小文补充了该函数图象上两个点![]() ,
,![]() .
.
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的大小是( )

A. 150° B. 130° C. 140° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(一6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.

(1)直接写出线段BO的长:
(2)求点D的坐标;
(3)若点N是平面内任一点,在x轴上是否存在点M,使咀M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.
(1)如图1,当有2个电子元件![]() 并联时,请你用树状图表示图中
并联时,请你用树状图表示图中![]() 之间电流能否通过的所有可能情况,并求出
之间电流能否通过的所有可能情况,并求出![]() 之间电流通过的概率;
之间电流通过的概率;
(2)如图2,当有3个电子元件并联时,求![]() 之间电流通过的概率.
之间电流通过的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com