
【题目】某市教育局为了了解该市九年级学生参加社会实践活动情况,随机抽查了某县部分九年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图.
请根据图中提供的信息,回答下列问题:
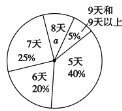
(1)![]() ________%,并写出该扇形所对圆心角的度数为________,请补全条形图;
________%,并写出该扇形所对圆心角的度数为________,请补全条形图;
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)若该县共有九年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
【答案】(1) 10,36°,补全统计图见解析;(2) 众数是5天; 中位数是6天;(3) 800.
【解析】
(1)根据扇形统计图中的数据可以求得a的值,进而求得该扇形所对圆心角的度数,然后再求出活动8天的人数即可将条形统计图补充完整;
(2)根据统计图中的数据可以直接写出众数和中位数;
(3)根据统计图中的数据可以估计“活动时间不少于7天”的学生人数大约有多少人.
(1)a=140%20%25%5%=10%,
该扇形所对圆心角的度数为:360°×10%=36°,
故答案为:10,36°;
调查的总人数是240÷40%=600人,
参加社会实践活动8天的人数为:600×10%=60,
补全的条形统计图如图所示;
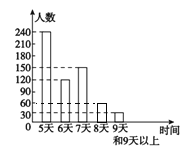
(2)由条形统计图可知,在这次抽样调查中,众数是5天,
第300,301人参加的天数为6天,故中位数是6天;
(3)2000×(25%+10%+5%)=800(人),
答:“活动时间不少于7天”的学生人数大约有800人.


科目:初中数学 来源: 题型:
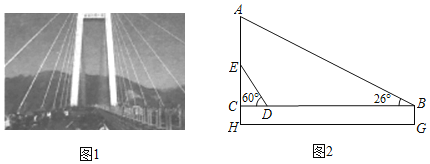
【题目】北盘江大桥坐落于云南宜威与贵州水城交界处,横跨云贵两省,为目前世界第一高桥图1是大桥的实物图,图2是从图1中引申出的平面图,测得桥护栏BG=1.8米,拉索AB与护栏的夹角是26°,拉索ED与护栏的夹角是60°,两拉索底端距离BD为300m,若两拉索顶端的距离AE为90m,请求出立柱AH的长.(tan26°≈0.5,sin26°≈0.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有6个白色乒乓球和若干个红色的乒乓球,这些球除颜色外其余均相同,搅拌均匀后,从这个袋子里随机摸出一个乒乓球,是红球的概率是![]()
(1)求该袋子中红球的个数;
(2)小亮取出3个白色乒乓球分别表上1,2,3个数字,装入另一个不透明的袋子里搅拌均匀,第一次从袋子里摸出一个球并记录下该球上的数字,重新放回袋子中搅拌均匀,第二次从袋子中摸出一个球并记录下该球上的数字,求这两个数字之积是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
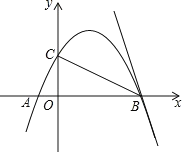
【题目】如图,抛物线y=ax2+bx+2经过点A(1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=![]() S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
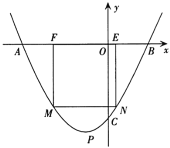
【题目】已知抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出点![]() 的坐标为________;
的坐标为________;
(2)如图,若![]() 、
、![]() 两点在原点的两侧,且
两点在原点的两侧,且![]() ,四边形
,四边形![]() 为正方形,其中顶点
为正方形,其中顶点![]() 、
、![]() 在
在![]() 轴上,
轴上,![]() 、
、![]() 位于抛物线上,求点
位于抛物线上,求点![]() 的坐标;
的坐标;
(3)若线段![]() ,点
,点![]() 为反比例函数
为反比例函数![]() 与抛物线
与抛物线![]() 在第一象限内的交点,设
在第一象限内的交点,设![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
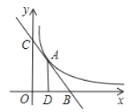
【题目】直线![]() 与双曲线
与双曲线![]() 只有一个交点A(1,2),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,
只有一个交点A(1,2),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,
求:(1)直线、双曲线的解析式.
(2)线段BC的长;
(3)三角形BOC的内心到三边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+b(k,b为常数,k≠0)与函数y=![]() 的图象交于点A(-1,m)
的图象交于点A(-1,m)
(1)求m;
(2)当k=______时,则直线l经过第一、三、四象限(任写一个符合题意的值即可);
(3)求(2)中的直线l的解析式和它与两坐标轴围成的三角形面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com