
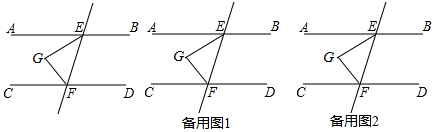
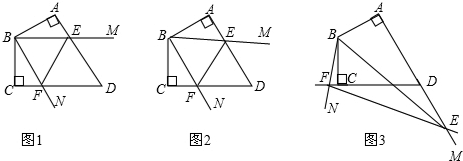
分析 (1)过点G作GP∥AB,根据平行线的性质,即可得出∠AEF+∠CFE=180°,∠AEG=∠EGP,∠CFG=∠FGP,再根据角平分线的定义,即可得到∠EGF=∠AEG+∠CFG=90°;
(2)分两种情况进行讨论:当点M在射线EA上时,由∠MGN=∠EGF=90°,可得∠MGE=∠NGF;当点M在射线EB上时,由∠MGN=∠EGF=90°,可得∠MGE=∠NGF;
(3)分两种情况进行讨论,根据角的和差关系以及两直线平行,内错角相等进行计算,即可得出∠CNG的度数.
解答 解:(1)如图,过点G作GP∥AB,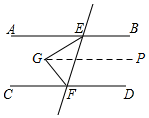
∵AB∥CD,
∴GP∥CD,
∴∠AEF+∠CFE=180°,∠AEG=∠EGP,∠CFG=∠FGP,
∵EG、FG分别是∠AEF和∠CFE的角平分线,
∴∠AEG=$\frac{1}{2}$∠AEF,∠CFG=$\frac{1}{2}$∠CFE,
∴∠AEG+∠CFG=$\frac{1}{2}$∠AEF+$\frac{1}{2}$∠CFE=$\frac{1}{2}$(∠AEF+∠CFE)=$\frac{1}{2}$×180°=90°,
∵∠EGF=∠EGP+∠FGP,
∴∠EGF=∠AEG+∠CFG=90°;
(2)如图,当点M在射线EA上时,由∠MGN=∠EGF=90°,可得∠MGE=∠NGF;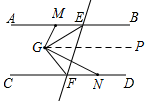
当点M在射线EB上时,由∠MGN=∠EGF=90°,可得∠MGE=∠NGF;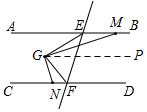
故答案为:∠MGE=∠NGF;
(3)当点M在射线EA上时,
∵∠MGE=∠NGF,∠MGE=20°,
∴∠EGN=∠MGN-∠MGE=90°-20°=70°,
∵AB∥GP,∠AEG=40°,
∴∠PGE=∠AEG=40°,
∴∠PGN=∠EGN-∠PGE=70°-40°=30°,
∵GP∥CD,
∴∠CNG=∠PGN=30°;
当点M在射线EB上时,
∵∠MGE=∠NGF,∠MGE=20°,
∴∠NGF=20°,
∴∠EGN=∠MGN+∠MGE=90°+20°=110°,
∵AB∥GP,∠AEG=40°,
∴∠PGE=∠AEG=40°,
∴∠PGN=∠EGN-∠PGE=110°-40°=70°,
∵GP∥CD,
∴∠CNG=∠PGN=70°,
综上所述:当∠MGE=20°,∠AEG=40°时,∠CNG=30°或70°.
点评 本题主要考查了平行线的性质,解决问题的关键是作辅助线构造内错角,依据两直线平行,内错角相等进行计算求解.解题时注意分类思想的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
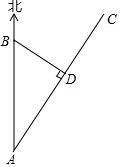 如图所示,沿海城市B的正南方向A处有一台风中心,沿AC的方向以30km/h的速度移动,已知AC所在的方向与正北成30°的夹角,B市距台风中心最短的距离BD为120km,求台风中心从A处到达D处需要多少小时?($\sqrt{3}≈1.73$,结果精确到0.1)
如图所示,沿海城市B的正南方向A处有一台风中心,沿AC的方向以30km/h的速度移动,已知AC所在的方向与正北成30°的夹角,B市距台风中心最短的距离BD为120km,求台风中心从A处到达D处需要多少小时?($\sqrt{3}≈1.73$,结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
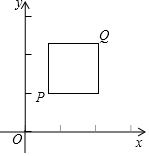 在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.
在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
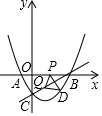 如图所示,抛物线y=ax2+bx-$\sqrt{3}$与x轴交于A,B两点,与y轴交于点C,其中A,B两点的坐标分别为(-1,0),(3,0).点P从点A出发,以每秒1个单位长度的速度沿线段AB向终点B运动;同时点Q从点B出发,以相同的速度沿线段BC向终点C运动,当一个动点到达终点时,另一个动点也随之停止运动,连接PQ.设点P运动的时间为t秒.
如图所示,抛物线y=ax2+bx-$\sqrt{3}$与x轴交于A,B两点,与y轴交于点C,其中A,B两点的坐标分别为(-1,0),(3,0).点P从点A出发,以每秒1个单位长度的速度沿线段AB向终点B运动;同时点Q从点B出发,以相同的速度沿线段BC向终点C运动,当一个动点到达终点时,另一个动点也随之停止运动,连接PQ.设点P运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com