
【题目】我们把具有一条公共边的两个三角形称为“友邻三角形”,两个三角形的公共边所对的顶点称为“友邻顶点”.
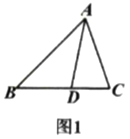
(1)如图1,写出图中所有的“友邻三角形”;
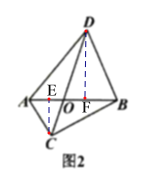
(2)如图2,![]() 与
与![]() 相交于点
相交于点![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求证:
,求证:![]() ;
;
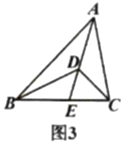
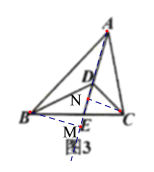
(3)从图3中找出两对“友邻三角形”,探索是否存在(2)中类似的结论,并直接写出结果;
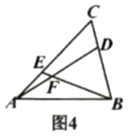
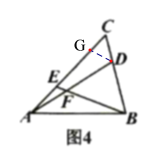
(4)如图4,![]() ,
,![]() ,若
,若![]() 的面积为21,求
的面积为21,求![]() 的面积.
的面积.
【答案】(1)![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() ;(2)见解析;(3)存在,
;(2)见解析;(3)存在,![]() 与
与![]() ,
,![]() 或
或![]() 与
与![]() ,
,![]() ;(4)6
;(4)6
【解析】
(1)根据“友邻三角形”的定义,即可得到答案;
(2)作![]() ,
,![]() ,易得COE~DOF,得
,易得COE~DOF,得![]() ,结合三角形的面积公式,即可得到结论;
,结合三角形的面积公式,即可得到结论;
(3)过点C作CN⊥AE于点E,过点B作BM⊥AE的延长线于点M,则CN∥BM,易得:BME~CNE,得![]() ,结合三角形的面积公式,
,结合三角形的面积公式,![]() ,同理得
,同理得![]() ;
;
(4)作![]() 交
交![]() 于
于![]() ,可得
,可得![]() ,从而得
,从而得![]() ,
,![]() ,进而即可求解.
,进而即可求解.
(1)根据“友邻三角形”的定义,可得图1中的“友邻三角形”为:![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() ;
;
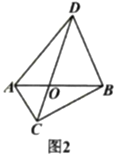
(2)作![]() ,
,![]() ,则CE∥DF,
,则CE∥DF,
∴COE~DOF,
∴![]() ,
,
∵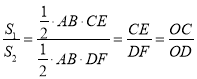 ;
;
(3)①![]() 与
与![]() ,
,![]() ,②
,②![]() 与
与![]() ,
,![]() ,理由如下:
,理由如下:
过点C作CN⊥AE于点E,过点B作BM⊥AE的延长线于点M,则CN∥BM,
∴BME~CNE,
∴![]() ,
,
∴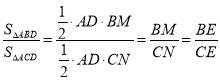 .
.
同理:![]() ;
;
(4)过点D作![]() ,
,
∴CG:CE=CD:BC=1:3,
∴设CG=x,则CE=3x,EG=2x,
∵![]() ,
,
∴AE=1.5x,
∴![]() ,即:
,即:![]() ,
,
∵![]() ,
,![]() 的面积为21,
的面积为21,
∴![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ×14=6.
×14=6.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
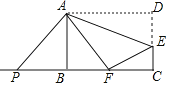
【题目】如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
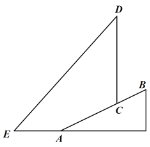
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知A![]() ,B
,B![]() 是一次函数y=kx+b与反比例函数
是一次函数y=kx+b与反比例函数![]() 图象的两个交点.
图象的两个交点.

(1) 根据图象回答:当x满足 ,一次函数的值小于反比例函数的值;
(2) 将直线AB沿y轴方向,向下平移n个单位,与双曲线![]() 有唯一的公共点时,求n的值;
有唯一的公共点时,求n的值;
(3) 如图2,P点在![]() 的图象上,矩形OCPD的两边OD、OC在坐标轴上,且OC=2OD,M、N分别为OC、OD的中点,PN与DM交于点E,直接写出四边形EMON的面积为 .
的图象上,矩形OCPD的两边OD、OC在坐标轴上,且OC=2OD,M、N分别为OC、OD的中点,PN与DM交于点E,直接写出四边形EMON的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十九大召开后,某社区开展了“市民对十九大的关注情况”调查,采用随机抽样的方法访问了部分年龄在18周岁以上的城乡居民.小聪根据调查数据绘制了如下不完整的频数分布置表和扇形统计图.请根据图表解答下列问题.
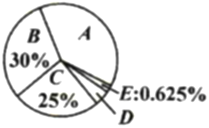
关注情况 | 频数 |
非常关注( | 128 |
比较关注( | |
一般关注( | 80 |
不太关注( | |
不关注( | 2 |
(1)请完成频数分布表空格数据填写;
(2)求“非常关注”部分扇形圆心角的度数;
(3)若该社区18周岁以上居民共有20000人,请估计“比较关注”和“非常关注”的居民共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
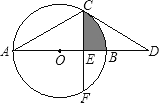
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学所在年级的500名学生参加志愿者活动,现有以下5个志愿服务项目:A,纪念馆志讲解员.B.书香社区图书整理C.学编中国结及义卖.D,家风讲解员E.校内志愿服务,要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:
收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图

选择各志愿服务项目的人数统计表
志愿服务项目 | 划记 | 人数 |
A.纪念馆志愿讲解员 | 正 | 8 |
B.书香社区图书整理 | ||
C.学编中国结及义卖 | 正正 | 12 |
D.家风讲解员 | ||
E.校内志愿服务 | 正 一 | 6 |
合计 | 40 | 40 |
分析数据、推断结论
(2)抽样的40个样本数据(志愿服务项目的编号)的众数是 (填A﹣E的字母代号)
(3)请你任选A﹣E中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的直径
的直径![]() ,点
,点![]() 是
是![]() 延长线上的一点,过
延长线上的一点,过![]() 点作
点作![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() .
.

(1)若![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,你认为
,你认为![]() 的大小是否发生变化?若变化,请说明理由;若不变化,求出
的大小是否发生变化?若变化,请说明理由;若不变化,求出![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com