
【题目】如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,过点C作CM∥BP交PA的延长线于点M.
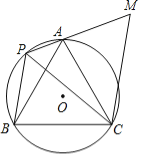
(1)求证:△ACM≌△BCP;
(2)若PA=1,PB=2,求△PCM的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)根据圆周角定理由∠APC=∠CPB=60°得∠BAC=∠ABC=60°,则△ABC是等边三角形,所以BC=AC,∠ACB=60°,再由CM∥BP得到∠PCM=∠BPC=60°,有可判断△PCM是等边三角形,得到PC=MC,∠M=60°,易得∠PCB=∠ACM,然后利用“AAS“可判断△ACM≌△BCP≌△ACM;
(2)由△ACM≌△BCP≌△ACM得AM=PB=2,则PM=PA+AM=3,由于△PCM是等边三角形,于是可根据等边三角形的性质计算其面积.
试题解析:(1)∵∠APC=∠CPB=60°,∴∠BAC=∠ABC=60°.∴△ABC是等边三角形.
∴BC=AC,∠ACB=60°.
∵CM∥BP,∴∠PCM=∠BPC=60°.
又∵∠APC=60°,∴△PCM是等边三角形. ∴PC=MC,∠M=60°.
∵∠BCA-∠PCA=∠PCM-∠PCA,∴∠PCB=∠ACM.
在△ACM和△BCP中,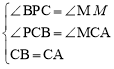 ,
,
∴△ACM≌△BCP≌△ACM(AAS).
(2)∵△ACM≌△BCP,∴AM=PB=2.∴PM=PA+AM=1+2=3.
∵△PCM是等边三角形,∴△PCM的面积=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求
,求![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .
.
根据你的观察,探究下面的问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知△ABC的三边长![]() ,且满足
,且满足![]() ,求c的取值范围;
,求c的取值范围;
(3)已知![]() ,
,![]() ,比较
,比较![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第一象限,⊙A与x轴交于B(2,0)、C(8,0)两点,与y轴相切于点D,则点A的坐标是( )
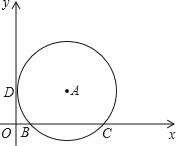
A. (5,4) B. (4,5) C. (5,3) D. (3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
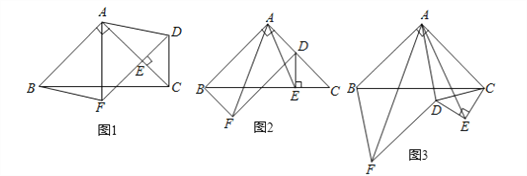
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
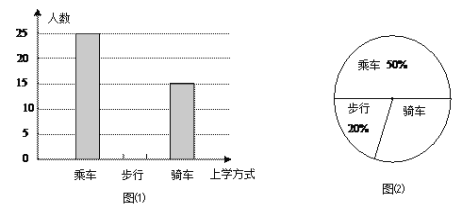
【题目】学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)求该班共有多少名学生;
(2)在图(1)中,将表示“步行”的部分补充完整;
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数;
(4)如果全年级共600名同学,请你估算全年级步行上学的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
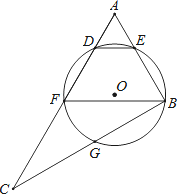
【题目】如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+![]() )π.
)π.
(1)求⊙O的半径;
(2)若DE∥BF,且AE=a,DF=2+![]() ﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.

(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图及探究:
已知:线段AB=a.
(1)完成尺规作图:

点P在线段AB所在直线上方,PA=PB,且点P到AB的距离等于![]() ,连接PA,PB,在线段AB上找到一点Q使得QB=PB,连接PQ,并直接回答∠PQB的度数;
,连接PA,PB,在线段AB上找到一点Q使得QB=PB,连接PQ,并直接回答∠PQB的度数;
(2)若将(1)中的条件“点P到AB的距离等于![]() ”替换为“PB取得最大值”,其余所有条件都不变,此时点P的位置记为
”替换为“PB取得最大值”,其余所有条件都不变,此时点P的位置记为![]() ,点Q的位置记为
,点Q的位置记为![]() ,连接
,连接![]() ,并直接回答∠
,并直接回答∠![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com