
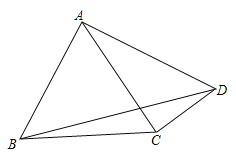
【题目】已知在四边形![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长度为________.
的长度为________.
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某课外学习小组根据学习函数的经验,对函数y=x3﹣3x的图象与性质进行了探究.请补充完整以下探索过程:
(1)列表:
x | … | ﹣2 |
| ﹣1 |
| 0 |
| 1 |
| 2 | … |
y | … | ﹣2 | m | 2 |
| 0 |
| n |
| 2 | … |
请直接写出m,n的值;
(2)根据上表中的数据,在平面直角坐标系内补全该函数的图象;
(3)若函数y=x3﹣3x的图象上有三个点A(x1,y1),B(x2,y2),C(x3,y3),且x1<﹣2<x2<2<x3,则y1,y2,y3之间的大小关系为 (用“<”连接);
(4)若方程x3﹣3x=k有三个不同的实数根.请根据函数图象,直接写出k的取值范围.
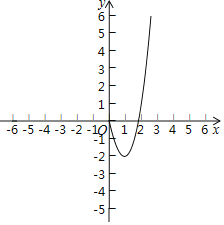
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,点P在以C(-2,0)为圆心,1为半径的圆上,Q是AP的中点
(k>0)的图象交于A、B两点,点P在以C(-2,0)为圆心,1为半径的圆上,Q是AP的中点
(1)若AO=![]() ,求k的值;
,求k的值;
(2)若OQ长的最大值为![]() ,求k的值;
,求k的值;
(3)若过点C的二次函数y=ax2+bx+c同时满足以下两个条件:①a+b+c=0;②当a≤x≤a+1时,函数y的最大值为4a,求二次项系数a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上, CE=CA,
AB,CE的延长线交于点F.
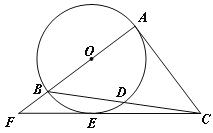
(1)求证:CE与⊙O相切;
(2)若⊙O的半径为3,EF=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③![]() 。其中正确的结论是____________.(填写所有正确结论的序号)
。其中正确的结论是____________.(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是以BC为直径的半圆的中点,连接AB,点D是直径BC上一点,连接AD,分别过点B、点C向AD作垂线,垂足为E和F,其中,EF=2,CF=6,BE=8,则AB的长是( )
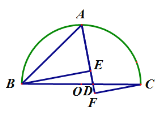
A.4B.6C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1:0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,求旗杆AB的高度约为多少?(保留一位小数,参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com