
����Ŀ����ȵ��������εĶ��壬���Ƕ��壺��һ���ڱ���ȵ��ı��ν��������ڱ��ı�������
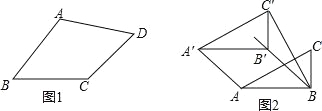
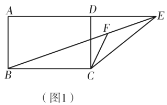
��1����ͼ 1�����ı��� ABCD �У�����һ������ʹ���ı��� ABCD �������ڱ��ı���������д�������ӵ�һ��������
��2��С����룺�Խ�����ƽ�ֵ������ڱ��ı����������Σ����IJ�����ȷ����˵�����ɣ�
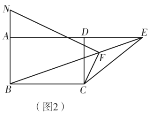
��3����ͼ 2��С������һ��Rt��ABC��������ABC��90�㣬AB��2��BC��1������ Rt��ABC ����ABC ��ƽ���� BB������ƽ�Ƶõ���A��B��C�������� AA�䣬 BC�䣮С��Ҫʹ��ƽ�ƺ���ı��� ABC��A���������ڱ��ı�������Ӧƽ�ƶ��پ��루���߶� B��B �ij�����
���𰸡���1��AB��BC �� BC��CD �� CD��AD �� AD��AB����2���⣺С��Ľ�����ȷ�����������������3��ƽ�� 2 ��![]() ��
��![]() ��
��![]() ��
��
��������
��1���ɡ����ڱ��ı��Ρ��Ķ����ó����ۣ�
��2����������ƽ���ı��ε��ж�������ƽ���ı��Σ������á����ڱ��ı��Ρ�������ڱ���ȣ��ó����ۣ�
����ƽ�Ƶ�������BB��=AA�䣬A��B���AB��A��B��=AB=2��B��C��=BC=1��A��C��=AC=5�������á����ڱ��ı��Ρ�����������ۣ��ɹ��ɶ����ó����ۣ�
��3������ת�����ʿɵá�ABF�ա�ADC����ȫ�����ʵ���ABF=��ADC����BAF=��DAC��AF=AC��FB=CD�����������������ж��á�ACF�ס�ABD�������Ƶ����ʺ��ı����ڽǺ͵á�CBF=90�㣬���ù��ɶ��������������ó����ۣ�
��1���⣺AB��BC �� BC��CD �� CD��AD �� AD��AB
��2���⣺С��Ľ�����ȷ��
�������£����ı��εĶԽ�����ƽ�֣�
������ı�����ƽ���ı��Σ�
���ı����������ڱ��ı�������
������ı�����һ���ڱ���ȣ�
����������ڱ��ı����������Σ�
��3���⣺����ABC��90����AB��2��BC��1���ã�AC�� ![]() ��
��
���� Rt��ABC ƽ�Ƶõ� Rt��A��B��C�䣬
��BA�䣽AA�䣬A��B���AB��A��B�䣽AB��2��B��C�䣽BC��1��A��C�䣽AC��![]() ��
��
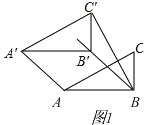
����ͼ 1���� AA�䣽AB ʱ��BB�䣽AA�䣽AB��2��

����ͼ 2���� AA�䣽A��C��ʱ��BB�䣽AA�䣽AC�䣽![]() ��
��
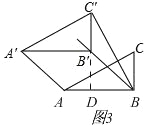
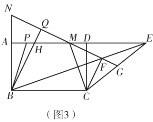
���� AC�䣽BC�䣽![]() ʱ����ͼ 3���ӳ� C��B���� AB �ڵ� D���� C��B���AB
ʱ����ͼ 3���ӳ� C��B���� AB �ڵ� D���� C��B���AB
��BB��ƽ����ABC��
���ABB���� ![]() ��ABC��45��
��ABC��45��
���BB��D����ABB�䣽45�㣬
��B��D��BD��
�� B��D��BD��x���� C��D��x+1��BB����![]() x
x
�������� Rt��BC��D ��BC��2��C��D2+BD2 �� x2+��x+1��2��5
��ã�x��1 �� x����2���������⣬��ȥ��
��BB�䣽![]()
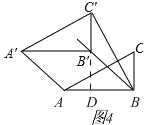
����BC����AB��2 ʱ����ͼ4������III������ͬ���ɵ���![]() ����ȥ��
����ȥ��
�� ![]() .
.
��Ӧƽ�� 2 ��![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ����
����![]() ��
��![]() ���ӳ����ϣ�����
���ӳ����ϣ�����![]() ��
��![]() ����
����![]() ��
��![]() ��ƽ����
��ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1����ͼ1����![]() �Ĵ�С��
�Ĵ�С��
��2����ͼ2������![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����֤��
����֤��![]() ��
��
��3����ͼ3���ڣ�2���������£�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() ����
����![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() ���ܳ���
���ܳ���![]() ���ܳ��IJ�Ϊ2����
���ܳ��IJ�Ϊ2����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
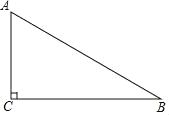
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣮
��1���ó߹��ڱ�BC������һ��P��ʹPA��PB����д������������ͼ�ۼ�����
��2������AP����APƽ�֡�CAB�����B�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ˮ���ڹ����ڼ䣬ÿСʱ�Ľ�ˮ���ͳ�ˮ�����ǹ̶�����ģ����賿4�㵽��8��ֻ��ˮ����ˮ��8�㵽12��Ƚ�ˮ�ֳ�ˮ��14�㵽�����賿ֻ��ˮ����ˮ����ͼ��ij��ˮ������ˮ��y�������ף���x��ʱ���ĺ���ͼ��
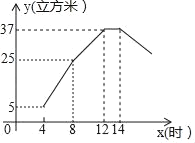
��1����ÿСʱ�Ľ�ˮ����
��2����8��x��12ʱ����y��x֮��ĺ�����ϵʽ��
��3���Ӹ����賿4�㵽�����賿����ˮ���е���ˮ����С��28������ʱ��ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
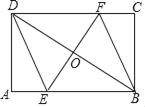
����Ŀ����ͼ���ھ���ABCD�У�AB=8��BC=4�����Խ���BD���е�O��ֱ�߷ֱ�AB��CD�ڵ�E��F������DE��BF��
��1����֤���ı���BEDF��ƽ���ı��Σ�
��2�����ı���BEDF������ʱ����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����Ϊ����3����6����������y=ax2+bx+c�����㣨��1����4���������н����д�����ǣ�������
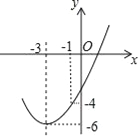
A. b2��4ac
B. ax2+bx+c�ݩ�6
C. ���㣨��2��m��������5��n�����������ϣ���m��n
D. ����x��һԪ���η���ax2+bx+c=��4������Ϊ��5�ͩ�1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺ֱ��![]() ��ֱ��
��ֱ��![]() ��Ϊ���Ѻ�ֱ�������磺ֱ��
��Ϊ���Ѻ�ֱ�������磺ֱ��![]() ��
��![]() ��Ϊ���Ѻ�ֱ������
��Ϊ���Ѻ�ֱ������
��1����![]() ��ֱ��
��ֱ��![]() �����Ѻ�ֱ�����ϣ���
�����Ѻ�ֱ�����ϣ���![]() ________��
________��
��2��ֱ��![]() �ϵĵ�
�ϵĵ�![]() �����������Ѻ�ֱ�����ϵĵ㣬���
�����������Ѻ�ֱ�����ϵĵ㣬���![]() �����ꣻ
�����ꣻ
��3������ֱ��![]() �ϵ�����һ��
�ϵ�����һ��![]() �����е�
�����е�![]() ���������Ѻ�ֱ�����ϣ���ֱ��
���������Ѻ�ֱ�����ϣ���ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
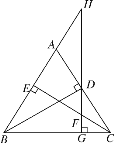
����Ŀ����ͼ��BD��CE�ֱ�����ABC�������ϵĸߣ���D��DG��BC��G���ֱ�CE��BA���ӳ�����F��H����֤��
(1)DG2��BG��CG��
(2)BG��CG��GF��GH.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ�������
A. ij�ֲ�Ʊ�н��ĸ�����![]() ����1000�Ÿ��ֲ�Ʊһ�����н�
����1000�Ÿ��ֲ�Ʊһ�����н�
B. �˽�һ�����ӻ���ʹ�������ʺ��ó�������
C. ���������ݵı���S��=0.31���������ݵı���S��=0.25�����������ݱȼ��������ȶ�
D. ��һ��װ�а��������Ĵ����������������Dz������¼�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com