
 一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10海里到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离(
一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10海里到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离( ≈1.4,
≈1.4, ≈1.7,结果保留整数).
≈1.7,结果保留整数).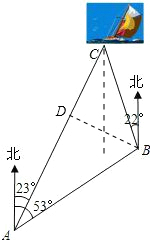 解:∵∠BAC=53°-23°=30°,
解:∵∠BAC=53°-23°=30°,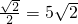 ≈7.0,
≈7.0,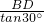 =5
=5 ÷
÷ =5
=5 ×
× =5
=5 ×
× ≈5×1.4×1.7≈11.9.
≈5×1.4×1.7≈11.9.

科目:初中数学 来源: 题型:
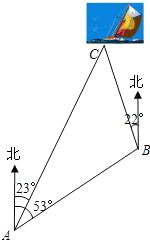 一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10海里到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离(
一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10海里到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离(| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
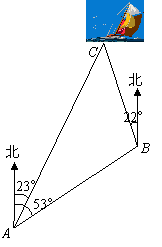
一艘小船从码头![]() 出发,沿北偏东
出发,沿北偏东![]() 方向航行,航行一段时间到达小岛
方向航行,航行一段时间到达小岛![]() 处后,又沿着北偏西
处后,又沿着北偏西![]() 方向航行了10海里到达
方向航行了10海里到达![]() 处,这时从码头测得小船在码头北偏东
处,这时从码头测得小船在码头北偏东![]() 的方向上,求此时小船与码头之间的距离(
的方向上,求此时小船与码头之间的距离(![]() ,结果保留整数).
,结果保留整数).
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
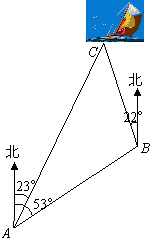
一艘小船从码头![]() 出发,沿北偏东
出发,沿北偏东![]() 方向航行,航行一段时间到达小岛
方向航行,航行一段时间到达小岛![]() 处后,又沿着北偏西
处后,又沿着北偏西![]() 方向航行了10海里到达
方向航行了10海里到达![]() 处,这时从码头测得小船在码头北偏东
处,这时从码头测得小船在码头北偏东![]() 的方向上,求此时小船与码头之间的距离(
的方向上,求此时小船与码头之间的距离(![]() ,结果保留整数).
,结果保留整数).
 |
查看答案和解析>>
科目:初中数学 来源:第1章《解直角三角形》中考题集(38):1.5 解直角三角形的应用(解析版) 题型:解答题
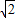 ≈1.4,
≈1.4,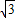 ≈1.7,结果保留整数).
≈1.7,结果保留整数).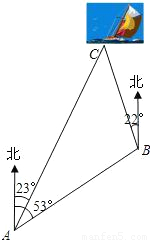
查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》中考题集(37):25.3 解直角三角形(解析版) 题型:解答题
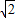 ≈1.4,
≈1.4,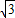 ≈1.7,结果保留整数).
≈1.7,结果保留整数).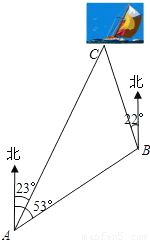
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com