
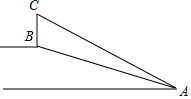
 某风景区在坡度为7:24的斜坡AB上有一座标志性建筑物BC.在点A处测得建筑物顶部C的仰角为31°.斜坡AB的长度为100米.则这座建筑物BC的高度约为( )(结果精确到0.1米,参考数据:sin31°≈0.52,tan31°≈0.60)
某风景区在坡度为7:24的斜坡AB上有一座标志性建筑物BC.在点A处测得建筑物顶部C的仰角为31°.斜坡AB的长度为100米.则这座建筑物BC的高度约为( )(结果精确到0.1米,参考数据:sin31°≈0.52,tan31°≈0.60)| A. | 21.9米 | B. | 29.6米 | C. | 35.0米 | D. | 57.6米 |
分析 由$\frac{BD}{AD}$=$\frac{7}{24}$可设BD=7x,AD=24x,利用勾股定理求得x即可知BD=28、AD=96,由CD=ADtan∠CAD≈57.6,根据BC=CD-BD可得答案.
解答 解:如图,延长CB交水平面于点D,
则∠CDA=90°,
由$\frac{BD}{AD}$=$\frac{7}{24}$可设BD=7x,AD=24x,
由BD2+AD2=AB2可得(7x)2+(24x)2=1002,
解得:x=4或x=-4(舍),
则BD=28,AD=96,
在Rt△ACD中,CD=ADtan∠CAD=96tan31°≈57.6,
∴BC=CD-BD=57.6-28≈29.6(米),
故选:B.
点评 本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 黄梅时节家家雨,青草池塘处处蛙 | B. | 人间四月芳菲尽,山寺桃花始盛开 | ||
| C. | 水面上秤锤浮,直待黄河彻底枯 | D. | 一夜北风紧,开门雪尚飘 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
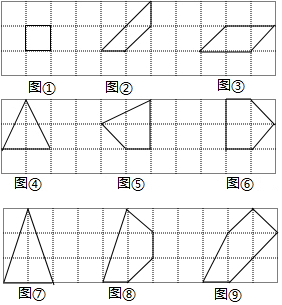
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ① | 0 | 4 | 1 |
| ② | 0 | 5 | 1.5 |
| ③ | 0 | 6 | 2 |
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ④ | 1 | 4 | 2 |
| ⑤ | 1 | 5 | 2.5 |
| ⑥ | 1 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
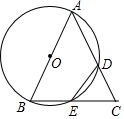 如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.
如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com