
【题目】A,B两点在数轴上的位置如图所示,其中O为原点,点A对应的有理数为﹣4,点B对应的有理数为6.
(1)动点P从点A出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒(t>0).
①当t=1时,AP的长为 ,点P表示的有理数为 ;
②当PB=2时,求t的值;
(2)如果动点P以每秒6个单位长度的速度从O点向右运动,点A和B分别以每秒1个单位长度和每秒3个单位长度的速度向右运动,且三点同时出发,那么经过几秒PA=2PB.
![]()
【答案】(1)①2,﹣2 ②t=6 (2) ①t=![]() 秒或16秒时, PA=2PB
秒或16秒时, PA=2PB
【解析】分析:(1)①根据路程=速度×时间,以及线段的和差定义计算即可;
②分两种情形分别求解即可;
(2)分两种情形:P在A、B之间或者P在B点右侧的情况,分别构建方程即可解决问题;
详解:(1)①∵动点P从点A出发,以每秒2个单位长度的速度向右运动,
∴当t=1时,AP=2,
∵OA=4,
∴OP=2,
∴点P表示的有理数为﹣2.
②当点P在B左侧时,∵AB=10,PB=2,
∴AP=8,
∴t=4.
当点P在点B右侧时,AP=12,
∴t=6;
(2)设一点时间为t秒;
①当P在A、B之间时,PA=4+6t=4+5t,PB=6+3t﹣6t=6﹣3t,
∵PA=2PB,
∴4+5t=2(6﹣3t),
解得t=![]() .
.
②当P点在B点右侧时,PA=4+5t,PB=3t﹣6,
∵PA=2PB,
∴4+5t=2(3t﹣6),
解得t=16,
故经过![]() 秒或16秒时,PA=2PB.
秒或16秒时,PA=2PB.


科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值其中结论正确的有( )
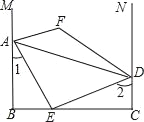
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: ![]() ≈1.7)
≈1.7)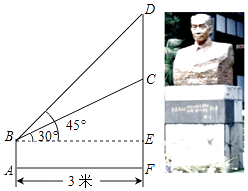
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠D=∠C=90°,E是DC的中点,AE平分∠DAB,∠DEA=28°,则∠ABE的度数是( )

A. 62° B. 31° C. 28° D. 25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线c1: ![]() 沿x轴翻折,得到抛物线c2 , 如图1所示.
沿x轴翻折,得到抛物线c2 , 如图1所示.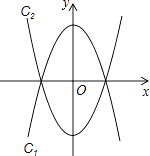
(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.
①当B、D是线段AE的三等分点时,求m的值;②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个底面直径为5 cm,高为18 cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com