
 ��ͼ����ֱ֪��y=x-5��������y=-x2+bx+c�ཻ��A��B���㣬��A�ĺ�����Ϊ-2����B��x���ϣ������C��D���߶�AB�ϵ��������㣬���ǵĺ�����ֱ���t��t+3������C��D�ֱ���ƽ����y���ֱ��CF��DE�������߷ֱ��ཻ�ڵ�F��E��
��ͼ����ֱ֪��y=x-5��������y=-x2+bx+c�ཻ��A��B���㣬��A�ĺ�����Ϊ-2����B��x���ϣ������C��D���߶�AB�ϵ��������㣬���ǵĺ�����ֱ���t��t+3������C��D�ֱ���ƽ����y���ֱ��CF��DE�������߷ֱ��ཻ�ڵ�F��E������ ��1����ȷ������A��B�����꣬���ô���ϵ������������߽���ʽ���ٱ�ʾ����C��D��E��F�����꣬�Ӷ���ʾ��CF��DE����������ı���CDEF��������ɵ�C��D�ĺ������ҵ�C��D���߶�AB�ϵó�t�ķ�Χ��
��2���ɣ�1���õ���C��D��E��F�����꣬��ʾ��CD��EF�����ı���CDEF�ǵ������εó�CD=EF��CF��DE�����������t��ֵ���ɣ�
��� �⣺��1����ͼ��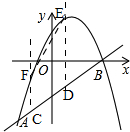 �ߵ�A�ĺ�����Ϊ-2������ֱ��y=x-5�ϣ�
�ߵ�A�ĺ�����Ϊ-2������ֱ��y=x-5�ϣ�
���A��������Ϊ-7��
��A��-2��-7����
�ߵ�B��ֱ��y=x-5�ϣ�����x���ϣ�
��B��5��0����
�ߵ�A��B��������y=-x2+bx+c�ϣ�
��$\left\{\begin{array}{l}{-7=-4-2b+c}\\{0=-25+5b+c}\end{array}\right.$��
��$\left\{\begin{array}{l}{b=4}\\{c=5}\end{array}\right.$��
�������ߵĽ���ʽΪy=-x2+4x+5��
�ߵ�C��D�ĺ�����Ϊt��t+3������ֱ��y=x-5��ͼ���ϣ�
��C��t��t-5����D��t+3��t-2����
��CF��y�ᣬDE��x�ᣬ
��F��t��-t2+4t+5����E��t+3��-t2-2t+8����
��CF=-t2+3t+10��DE=-t2-3t+10��
��S�ı���CDEF=$\frac{1}{2}$��CF+DE����3=$\frac{1}{2}$[-t2+3t+10+��-t2-3t+10��]��3=-3t2+30��
�ߵ�C��D���߶�AB�ϣ�
��t��-2��t+3��5��
��-2��t��2
��S�ı���CDEF=-3t2+30����-2��t��2��
��2���ı���CDEF���ܳ�Ϊһ���������Σ�
�����ı���CDEF�ǵ������Σ�
��CD=EF��CF��DE
��C��t��t-5����D��t+3��t-2����
��CD2=9+9=18��
��F��t��-t2+4t+5����E��t+3��-t2-2t+8����
��EF2=9+��6t-3��2��
��9+��6t-3��2=18��
��t=0��t=1��
-t2+3t+10��-t2-3t+10��
��t��0��
��t=1��
����t=1���ı���CDEF�ǵ������Σ�
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ���������ε������ƽ������ϵ�������ľ��빫ʽ�����εĶ��壬�Ȿ��Ĺؼ�����t��ʾ��CF��DE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �߶� | B�� | �ȱ������� | C�� | ƽ���ı��� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ı���ABCD�У�AD��BC����B=90�㣬EΪAB��һ�㣬�ֱ���ED��ECΪ�ۺ۽���A����B�������𣬵�A��Bǡ������CD�ߵĵ�F������AD=3��BC=5����EF=$\sqrt{15}$��
�ı���ABCD�У�AD��BC����B=90�㣬EΪAB��һ�㣬�ֱ���ED��ECΪ�ۺ۽���A����B�������𣬵�A��Bǡ������CD�ߵĵ�F������AD=3��BC=5����EF=$\sqrt{15}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com