练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．在正方形ABCD所在的平面内找一点P，使其与正方形中的每一边所构成的三角形均为等腰三角形，这样的点有5个．

    分析 作正方形与边平行的两条对称轴，两对称轴的交点为P点，然后分别以正方形的各边向外作等边三角形，则第三个顶点为P点．

    解答 解：如图，满足条件的P点有5个．
    ∁
    故答案为5．

    点评 本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．某电信公司提供的移动通讯服务的收费标准有两种方案，如表所示：
    A方案B方案
    每月基本服务费30元50元
    每月免费通话时间120分200分
    超出后每分钟收费0.4元0.4元
    设每月通话时间为x分，A，B两种方案每月话费分别为y1元，y2元．
    （1）分别写出当x＞120时，y1关于x的函数表达式和当x＞200时，y2关于x的函数表达式；
    （2）在如图所示的平面直角坐标系中，把y1和y2这两个函数图象的其余部分补画出来；（实线为A方案，虚线为B方案）
    （3）结合图象考虑，若以节省费用的角度考虑，则应如何选择最优方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，点E，F在BC上，BE=CF，∠AFE=∠DEF，∠B=∠C，求证：AB=DC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．已知CD为⊙O的直径，M为OD的中点，AB⊥CD于M，若AB=4，则⊙O的直径CD=$\frac{4\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图所示，已知等边△ABC中，AB=AC=BC，∠CAB=∠CBA=∠C=60°，BD=CE，AD与BE相交于点P，则∠APE=60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

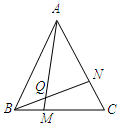    2．（1）学完全等三角形以后，老师布置了这样一道题：如图，点M、N分别在等边△ABC的BC、CA边上，且BM=CN，AM、BN交于点Q．求证：∠BQM=60°．（注意：等边三角形三条边都相等，每个内角都是60°）
    （2）小丽做完后，进行了反思，提出了许多问题，如：
    ①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题？
    ②若将题中的点M、N分别移动到BC、CA的延长线上，是否仍能得到∠BQM=60°？
    请你作出判断，在下列横线上填写“是”或“否”：①是；②是．并对上述真命题选择一个给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，AB为⊙O的直径，点D在⊙O上，∠BAC=35°，则∠ADC=55°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．用“＜”“＞”或“=”填空：-6＜0，-1＞-10，-|-4|=-4，-π＜-3.14．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．因式分解
    （1）a3x2-a3y2
    （2）x2（x-y）+（y-x）
    （3）m2-2mn+n2-9．

    查看答案和解析>>

    同步练习册答案