
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上(但不与A点重合),求t的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据中垂线性质可知,作AB的垂直平分线,与AC交于点P,则满足PA=PB,在Rt△ABC中,用勾股定理计算出AC=8cm,再用t表示出PA=t cm,则PC=![]() cm,在Rt△PBC中,利用勾股定理建立方程求t;
cm,在Rt△PBC中,利用勾股定理建立方程求t;
(2)过P作PD⊥AB于D点,由角平分线性质可得PC=PD,由题意PC=![]() cm,则PB=
cm,则PB=![]() cm,在Rt△ABD中,利用勾股定理建立方程求t.
cm,在Rt△ABD中,利用勾股定理建立方程求t.
(1)作AB的垂直平分线交AB于D,交AC于P,连接PB,如图所示,
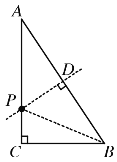
由垂直平分线的性质可知PA=PB,此时P点满足题意,
在Rt△ABC中,![]() cm,
cm,
由题意PA= t cm,PC=![]() cm,
cm,
在Rt△PBC中,![]() ,
,
即![]() ,解得
,解得![]()
(2)作∠CAB的平分线AP,过P作PD⊥AB于D点,如图所示
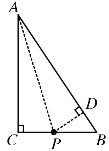
∵AP平分∠CAB,PC⊥AC,PD⊥AB,
∴PC=PD
在Rt△ACP和Rt△ADP中,
![]()
∴![]()
∴AD=AC=8cm
∴BD=AB-AD=10-8=2cm
由题意PD=PC=![]() cm,则PB=
cm,则PB=![]() cm,
cm,
在Rt△ABD中,![]()
即![]()
解得![]()


科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,则不一定能使△ABD≌△ACD的条件是( )

A.BD=DCB.∠ABD=∠ACD=90°C.∠BDA=∠CDAD.∠BAD=∠CAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全教育,某校组织了“防溺水”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍![]() 购买2副乒乓球拍和1副羽毛球拍共需116元;购买3副乒乓球拍和2副羽毛球拍共需204元.
购买2副乒乓球拍和1副羽毛球拍共需116元;购买3副乒乓球拍和2副羽毛球拍共需204元.
![]() 求购买1副乒乓球拍和1副羽毛球拍各需多少元;
求购买1副乒乓球拍和1副羽毛球拍各需多少元;
![]() 若学校购买乒乓球拍和羽毛球拍共30副,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
若学校购买乒乓球拍和羽毛球拍共30副,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若△ABC 、△AMN周长分别为13cm和8cm.

(1)求证:△MBE为等腰三角形;
(2)线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解方程x2﹣![]() x+1=0的时候,奇奇的方法别出心裁:
x+1=0的时候,奇奇的方法别出心裁:
解:移项得:x2+1=![]() x,变形得:x2+1=
x,变形得:x2+1=![]() x=(
x=(![]() +
+![]() )x①,由于原方程中x≠0,故可以在①的两边同时除以x得:x+
)x①,由于原方程中x≠0,故可以在①的两边同时除以x得:x+![]() =
=![]() +
+![]() 解得:x1=
解得:x1=![]() ,x2=
,x2=![]()
这是利用对称式的典型范例,下面的问题需要你来完成:
(1)直接写出方程x﹣![]() =b﹣
=b﹣![]() 的解:
的解:
(2)由(1)的结论解关于x的方程:x﹣![]() =a﹣
=a﹣![]() (a≠2)
(a≠2)
(3)模仿奇奇的解法,解方程:x2﹣![]() x+4=0.
x+4=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和40,则△EDF的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
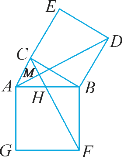
【题目】如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连接AD、CF,AD与CF交于点M,AB与CF交于点H.
(1)求证:△ABD≌△FBC;
(2)已知AD=6,求四边形AFDC的面积;
(3)在△ABC中,设BC=a,AC=b,AB=c,当∠ACB≠90°时,c![]() ≠a
≠a![]() +b
+b![]() .在任意△ABC中,c
.在任意△ABC中,c![]() =a
=a![]() +b
+b![]() +k.就a=3,b=2的情形,探究k的取值范围(只需写出你得到的结论即可).
+k.就a=3,b=2的情形,探究k的取值范围(只需写出你得到的结论即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com