
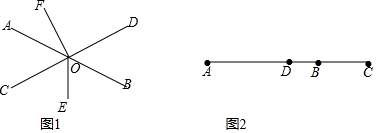
分析 (1)根据平角的定义得出∠AOF和∠BOC的度数,再由角平分线的定义得出∠COE的度数.
(2)根据点D为AC的中点得出AC=2DC,再由BC=$\frac{1}{2}$AB,得AB=2BC,即可得出AB的长.
解答 解:(1)∵∠AOC+∠AOF+∠DOF=180°,
∴∠AOF=180°-∠AOC-∠DOF.
∵∠AOC=62°46′,∠DOF=90°,
∴∠AOF=180°-62°46′-90°=27°14′.
∵∠AOC+∠BOC=180°,
∴∠BOC=180°-∠AOC
=180°-62°46′=117°14′.
∵射线OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×117°14′=58°37′.
(2)∵D为AC的中点,
∴AC=2DC=2×2=4(cm).
∵BC=$\frac{1}{2}$AB,
∴AB=2BC.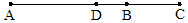
∵AC=AB+BC=3BC,
∴AB=$\frac{2}{3}$AC=$\frac{2}{3}$×4=$\frac{8}{3}$(cm).
∴AB的长为$\frac{8}{3}$cm.
点评 本题考查了角平分线的定义以及两点之间的距离,以及度分秒的换算,掌握计算方法是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不等式的两边都加上(或减去)同一个整式,不等号的方向不变 | |
| B. | 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变 | |
| C. | 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变 | |
| D. | 以上答案均不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h,有下列四种说法:①a•b=c•h;②a+b<c+h;③以a+b、h、c+h为边的三角形,是直角三角形;④$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$.其中正确的有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h,有下列四种说法:①a•b=c•h;②a+b<c+h;③以a+b、h、c+h为边的三角形,是直角三角形;④$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
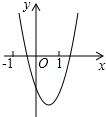 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+$\frac{b}{2a}$与反比例函数y=abx-1在同一坐标系内的大致图象是( )
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+$\frac{b}{2a}$与反比例函数y=abx-1在同一坐标系内的大致图象是( )| A. |  | B. | 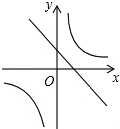 | C. | 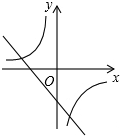 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com